
抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
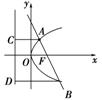
如图所示,依题意,设抛物线方程为y2=2px,则直线方程为y=-x+p.设直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B分别作准线的垂线,垂足分别为C、D.
则由抛物线定义得
|AB|=|AF|+|FB|=|AC|+|BD|
=x1++x2+,………………4分
即x2++x2+=8.①
又A(x1,y1)、B(x2,y2)是抛物线和直线的交点,
由消去y,得x2-3px+=0,
Δ=9p2-4×=8p2>0.
所以x1+x2=3p.
将其代入①得p=2,
所以所求抛物线方程为y2=4x.
当抛物线方程设为y2=-2px(p>0)时,
同理可求得抛物线方程为y2=-4x.
故所求抛物线方程为y2=4x或y2=-4x.………………8分
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
(2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.查看答案和解析>>
科目:高中数学 来源: 题型:
 实轴长为4
实轴长为4| 3 |
| AC |
| AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com