
【题目】某高校数学学院为了对2018年录取的大一新生有针对性地进行教学.从大一新生中随机抽取40名,对他们在2018年高考的数学成绩进行调查,统计发现40名新生的数学分数![]() 分布在
分布在![]() 内.当
内.当![]() 时,其频率
时,其频率![]() .
.

(1)求![]() 的值;
的值;
(2)请在答题卡中画出这40名新生高考数学分数的频率分布直方图,并估计这40名新生的高考数学分数的平均数(同一组中的数据用该区间的中点值作代表).
(3)若高考数学分数不低于120分的为优秀,低于120分的为不优秀,则按高考成绩优秀与否从这40名新生中用分层抽样的方法抽取4名学生,再从这4名学生中随机抽取2名,求这2名学生的高考成绩均为优秀的概率.
【答案】(1)![]() ; (2)直方图见解析,
; (2)直方图见解析,![]() ; (3)
; (3)![]() .
.
【解析】
(1)![]() 的取值为10,11,12,13,14,把
的取值为10,11,12,13,14,把![]() 的取值分别代入
的取值分别代入![]() ,根据频率的和为1,列方程求解即可;(2)利用频率除以组距可得纵坐标,从而可得直方图,每个矩形的中点横坐标与该矩形的纵坐标及组距相乘后求和可得平均值;(3)利用列举法,列举出从这4名学生中随机抽取2名的事件,以及其中这2名学生的高考成绩均为优秀的事件,由古典概型概率公式可得结果.
,根据频率的和为1,列方程求解即可;(2)利用频率除以组距可得纵坐标,从而可得直方图,每个矩形的中点横坐标与该矩形的纵坐标及组距相乘后求和可得平均值;(3)利用列举法,列举出从这4名学生中随机抽取2名的事件,以及其中这2名学生的高考成绩均为优秀的事件,由古典概型概率公式可得结果.
(1)由题意知,![]() 的取值为10,11,12,13,14.
的取值为10,11,12,13,14.
把![]() 的取值分别代入
的取值分别代入![]() ,可得
,可得
![]() .
.
解得![]() .
.
(2)频率分布直方图如图,

这40名新生的高考数学分数的平均数为![]() .
.
(3)这40名新生的高考数学分数在![]() 的频率为
的频率为![]() ,所以高考数学成绩不优秀和优秀的频率比
,所以高考数学成绩不优秀和优秀的频率比![]() .按高考数学成绩优秀与否分层抽样的方法从40名学生中抽取的4名学生中有3名学生高考成绩优秀,
.按高考数学成绩优秀与否分层抽样的方法从40名学生中抽取的4名学生中有3名学生高考成绩优秀,
记![]() 为4名学生,其中
为4名学生,其中![]() 为3名高考数学成绩优秀的学生.
为3名高考数学成绩优秀的学生.
从4名学生中随机抽取2名学生的基本事件为![]() ,共6个,
,共6个,
2名学生高考数学成绩均优秀的事件为![]() ,共3个,
,共3个,
故所求的概率为![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,
,![]() 分别是椭圆的左、右两焦点,过
分别是椭圆的左、右两焦点,过![]() 且倾斜角为
且倾斜角为![]() (
(![]() )的动直线
)的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(如图所示,点
两点(如图所示,点![]() 在
在![]() 轴上方).当
轴上方).当![]() 时,弦
时,弦![]() 的长为
的长为![]() .
.

(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)若![]() 依次成等差数列,求直线
依次成等差数列,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“吃鸡”游戏中,某玩家被随机降落在边长为4的正三角形绝地岛上,已知在离三个顶点距离都大于![]() 的区域内可以搜集枪支弹药、防弹衣、医疗包等生存物资,则该玩家能够获得生存物资的概率为( )
的区域内可以搜集枪支弹药、防弹衣、医疗包等生存物资,则该玩家能够获得生存物资的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值.
处取得最大值.
(1)求![]() 的最小值,并求出此时函数
的最小值,并求出此时函数![]() 的解析式和最小正周期;
的解析式和最小正周期;
(2)在(1)的条件下,先将![]() 的图像上的所有点向右平移
的图像上的所有点向右平移![]() 个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),然后将所得图像上所有的点向下平移
个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),然后将所得图像上所有的点向下平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像.若在区间
的图像.若在区间![]() 上,方程
上,方程![]() 有两个不相等的实数根,求实数a的取值范围;
有两个不相等的实数根,求实数a的取值范围;
(3)在(1)的条件下,已知点P是函数![]() 图像上的任意一点,点Q为函数
图像上的任意一点,点Q为函数![]() 图像上的一点,点
图像上的一点,点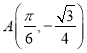 ,且满足
,且满足![]() ,求
,求![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com