
【题目】如图,在三棱柱![]() 中,
中, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() 为侧棱
为侧棱![]() 上的动点.
上的动点.

(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(![]() )试判断直线
)试判断直线![]() 与平面
与平面![]() 是否能够垂直.若能垂直,求
是否能够垂直.若能垂直,求![]() 的值,若不能垂直,请说明理由.
的值,若不能垂直,请说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】试题分析:(1)由已知推导出![]() ,
, ![]() ,故而可得
,故而可得![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;(2)取
;(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,
, ![]() ,可得到四边形
,可得到四边形![]() 为平行四边形,紧接着证明平面
为平行四边形,紧接着证明平面![]() 平面
平面![]() ,故而可得结论;(3)假设
,故而可得结论;(3)假设![]() 平面
平面![]() ,则
,则![]() ,首先证明
,首先证明![]() ,接着得到
,接着得到![]() ,然后根据
,然后根据![]() 得到
得到![]() ,,从而得到直线
,,从而得到直线![]() 与平面
与平面![]() 不能垂直.
不能垂直.
试题解析:(![]() )证明:由已知,三棱柱
)证明:由已知,三棱柱![]() 为直三棱柱,∴
为直三棱柱,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]() ,
, ![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(![]() )证明:取
)证明:取![]() 中点
中点![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,∴
中点,∴![]() ,同理
,同理![]() ,
,
∴![]() ,∴
,∴![]() 平面
平面![]() ,连结
,连结![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 中点,∴
中点,∴![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.

(![]() )若
)若![]() 平面
平面![]() ,则
,则![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() 即
即![]() ,
,
∴![]() ,与
,与![]() 为棱
为棱![]() 上一点矛盾,∴直线
上一点矛盾,∴直线![]() 与平面
与平面![]() 不能垂直.
不能垂直.


科目:高中数学 来源: 题型:
【题目】对某班一次测验成绩进行统计,如下表所示:
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
概率 | 0.02 | 0.04 | 0.17 | 0.36 | 0.25 | 0.15 |
(1)求该班成绩在[80,100]内的概率;
(2)求该班成绩在[60,100]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )
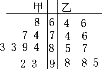
A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 分别是
分别是![]() 的边
的边![]() 的中点,连接
的中点,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠至
折叠至![]() 的位置,连接
的位置,连接![]() .记平面
.记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角大小.
所成锐二面角大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂抽取50名工人进行调查,发现他们一天加工零件的个数在50至350之间,现按生产的零件个数将他们分成六组,第一组[50,100),第二组[100,150),第三组[150,200),第四组[200,250),第五组[250,300),第六组[300,350],相应的样本频率分布直方图如图所示.
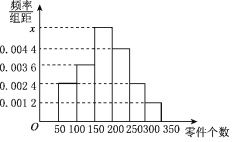
(1)求频率分布直方图中x的值;
(2)设位于第六组的工人为拔尖工,位于第五组的工人为熟练工,现用分层抽样的方法在这两类工人中抽取一个容量为6的样本,从样本中任意取两个,求至少有一个拔尖工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
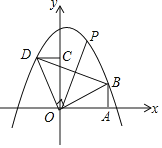
【题目】如图所示,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到![]() ,抛物线
,抛物线![]() 经过B、D两点.
经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com