
【题目】如图,已知点![]() 分别是
分别是![]() 的边
的边![]() 的中点,连接
的中点,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠至
折叠至![]() 的位置,连接
的位置,连接![]() .记平面
.记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角大小.
所成锐二面角大小.

【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)由![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,根据三角形中位线定理可得
的中点,根据三角形中位线定理可得![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,再利用线面平行的性质定理可得结论;(2)由三角形中位线定理以可判定四边形
,再利用线面平行的性质定理可得结论;(2)由三角形中位线定理以可判定四边形![]() 平行四边形,进而可得四边形
平行四边形,进而可得四边形![]() 为菱形,于是可得
为菱形,于是可得![]() ,
, ![]() ,
,![]()
![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,从而根据面面垂直的判定定理可得结论;(3)作
,从而根据面面垂直的判定定理可得结论;(3)作![]() 于
于![]() 交
交![]() 于
于![]() ,可知
,可知![]() 是
是![]() 的中点,折叠后角
的中点,折叠后角![]() 是二面角
是二面角![]() 的平面角,可证明等腰
的平面角,可证明等腰![]() 的底角
的底角![]() 是平面
是平面![]() 与平面
与平面![]() 所成锐二面角的平面角,进而可得结果.
所成锐二面角的平面角,进而可得结果.
试题解析:(1)证明:∵![]() 且
且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∵经过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
∴![]() ,
,
又∵![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
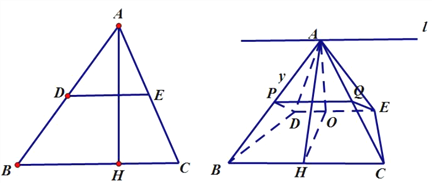
(2)延长![]() ,
, ![]() 相交于
相交于![]() ,连接
,连接![]()
∵![]() ,
,
∴![]() ,同理知
,同理知![]()
∴![]() 平面
平面![]() ,又由
,又由![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
(3)过点![]() 作
作![]() 于
于![]() ,
, ![]() 交
交![]() 于
于![]() ,易知
,易知![]() 是
是![]() 的中点,
的中点,
易知折叠后角![]() 是二面角
是二面角![]() 的平面角
的平面角
∴角![]() ,且
,且![]() 平面
平面![]() ,连接
,连接![]() ,由(1)知
,由(1)知![]() ,
,
则可知![]() 平面
平面![]() .
.
∴![]() ,且
,且![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,易知
,易知![]()
∴等腰![]() 的底角
的底角![]() 是平面
是平面![]() 与平面
与平面![]() 所成锐二面角的平面角,
所成锐二面角的平面角,
易知角![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
(Ⅰ)证明:OB⊥EH;
(Ⅱ)若直线BH与平面EFG所成的角的正弦值为 ![]() ,求二面角D﹣AC﹣H的余弦值.
,求二面角D﹣AC﹣H的余弦值.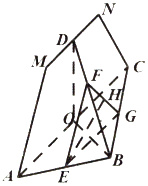
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() 为侧棱
为侧棱![]() 上的动点.
上的动点.

(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(![]() )试判断直线
)试判断直线![]() 与平面
与平面![]() 是否能够垂直.若能垂直,求
是否能够垂直.若能垂直,求![]() 的值,若不能垂直,请说明理由.
的值,若不能垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣2|+|x﹣a|,x∈R.
(Ⅰ)求证:当a=﹣1时,不等式lnf(x)>1成立;
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且有|PQ|=|PA|.
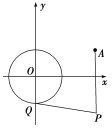
(1)求a,b间的关系;
(2)求|PQ|的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于十进制中的逢10进1,十二进制的进位原则是逢12进1,采用数字0,1,2,…,9和字母M,N作为计数符号,这些符号与十进制的数字对应关系如下表:
十二进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | M | N |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
例如,因为563=3×122+10×12+11,所以十进制中的563在十二进制中被表示为3MN(12).那么十进制中的2008在十二进制中被表示为( )
A. 11N4(12) B. 1N25(12) C. 12N4(12) D. 1N24(12)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() =0.
=0.
(1)若a是从集合A={x∈Z|0≤x≤3}中任取一个元素,b是从集合B={x∈Z|0≤x≤2}中任取一个元素,求方程![]() =0恰有两个不相等实根的概率;
=0恰有两个不相等实根的概率;
(2) 若a是从集合A={x|0≤x≤3}中任取一个元素,b是从集合B={x|0≤x≤2}中任取一个元素,求上述方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com