
【题目】如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
(Ⅰ)证明:OB⊥EH;
(Ⅱ)若直线BH与平面EFG所成的角的正弦值为 ![]() ,求二面角D﹣AC﹣H的余弦值.
,求二面角D﹣AC﹣H的余弦值.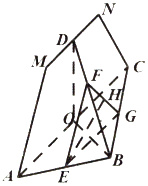
【答案】解:(Ⅰ)证明:因为点O、D分别是等腰梯形AMNC两底AC、MN的中点,所以OD⊥OC.又AB=BC,
则OB⊥AC.于是等腰梯形AMNC与直角△ABC所成二面角的平面角为∠BOC,则∠BOC= ![]() .即OB⊥OD,得OB⊥平面AMNC.
.即OB⊥OD,得OB⊥平面AMNC.
又平面AMNC∥平面EFG,则OB⊥平面EFG.
因为EG平面EFG,所以OB⊥EH.
(Ⅱ)以O为原点,分别以 ![]() 为x轴、y轴、z轴
为x轴、y轴、z轴
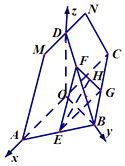
的正方向,建立空间直角坐标系,如图所示.
设OA=a,OB=b,则O(0,0,0),A(a,0,0),B(0,a,0),D(0,0,b),C(﹣a,0,0).
所以E( ![]() ,F(0,
,F(0, ![]() ),G(﹣
),G(﹣ ![]() ,H(﹣
,H(﹣ ![]() ),有
),有 ![]() ,平面EFG的一个法向量为
,平面EFG的一个法向量为 ![]() .
.
设直线BH与平面EFG所成的角为α,则sinα=|cos< ![]() |=
|= 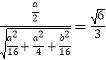 ,得a=b.
,得a=b.
设平面HAC的法向量为 ![]() ,由
,由 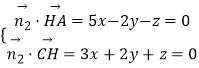 ,取y=1,得
,取y=1,得 ![]() ,
,
所以cos< ![]() >=
>= ![]() ,
,
因为二面角D﹣AC﹣H为锐二面角,所以二面角D﹣AC﹣H的余弦值为 ![]() .
.
【解析】(Ⅰ)由题意知等腰梯形AMNC与直角△ABC所成二面角的平面角为∠BOC,则∠BOC= ![]() . 得OB⊥平面AMNC.又平面AMNC∥平面EFG,则OB⊥平面EFG即可.(Ⅱ)以O为原点,分别以
. 得OB⊥平面AMNC.又平面AMNC∥平面EFG,则OB⊥平面EFG即可.(Ⅱ)以O为原点,分别以 ![]() 为x轴、y轴、z轴的正方向,建立空间直角坐标系,如图所示.
为x轴、y轴、z轴的正方向,建立空间直角坐标系,如图所示.
设OA=a,OB=b,则O(0,0,0),A(a,0,0),B(0,a,0),D(0,0,b),C(﹣a,0,0).利用向量法求解.
【考点精析】认真审题,首先需要了解空间中直线与直线之间的位置关系(相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率为
的中心在原点,离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆下顶点为![]() ,直线
,直线![]() (
(![]() )与椭圆相交于不同的两点
)与椭圆相交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(﹣t)+4034t+2017,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )
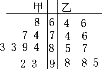
A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 分别是
分别是![]() 的边
的边![]() 的中点,连接
的中点,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠至
折叠至![]() 的位置,连接
的位置,连接![]() .记平面
.记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角大小.
所成锐二面角大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若![]() ,
, ![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑤设![]() ,则函数
,则函数![]() 的最小值是
的最小值是![]() ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com