
【题目】已知关于![]() 的方程
的方程![]() ,根据下列条件,分别求出
,根据下列条件,分别求出![]() 的值.
的值.
(1)方程两实根的积为5;
(2)方程的两实根![]() 满足
满足![]() .
.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , an>0,且满足:(an+2)2=4Sn+4n+1,n∈N* .
(1)求a1及通项公式an;
(2)若bn=(﹣1)nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,曲线![]() 由上半椭圆
由上半椭圆![]() 和部分抛物线
和部分抛物线![]()
![]() 连接而成,
连接而成, ![]() 的公共点为
的公共点为![]() ,其中
,其中![]() 的离心率为
的离心率为![]() .
.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 分别交于
分别交于![]() (均异于点
(均异于点![]() ),若
),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,连接
的中点,连接![]() .现将
.现将![]() 沿
沿![]() 折叠至Δ
折叠至Δ![]() 的位置,连接
的位置,连接![]() .记平面
.记平面 ![]() 与平面
与平面 ![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.


(1)证明: ![]()
(2)证明: ![]()
(3)求平面![]() 与平面
与平面 ![]() 所成锐二面角大小.
所成锐二面角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
(Ⅰ)证明:OB⊥EH;
(Ⅱ)若直线BH与平面EFG所成的角的正弦值为 ![]() ,求二面角D﹣AC﹣H的余弦值.
,求二面角D﹣AC﹣H的余弦值.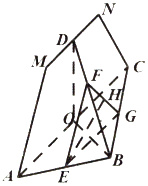
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于十进制中的逢10进1,十二进制的进位原则是逢12进1,采用数字0,1,2,…,9和字母M,N作为计数符号,这些符号与十进制的数字对应关系如下表:
十二进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | M | N |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
例如,因为563=3×122+10×12+11,所以十进制中的563在十二进制中被表示为3MN(12).那么十进制中的2008在十二进制中被表示为( )
A. 11N4(12) B. 1N25(12) C. 12N4(12) D. 1N24(12)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com