
【题目】如图,已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且有|PQ|=|PA|.
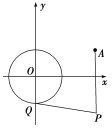
(1)求a,b间的关系;
(2)求|PQ|的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
【答案】(1)2a+b-3=0(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)由勾股定理可得 PQ2=OP2﹣OQ2=PA2,即 (a2+b2)﹣1=(a﹣2)2+(b﹣1)2,化简可得a,b间满足的等量关系.
(2)由于 PQ=![]() =
=![]() ,利用二次函数的性质求出它的最小值.
,利用二次函数的性质求出它的最小值.
(3)设⊙P 的半径为R,可得|R﹣1|≤PO≤R+1.利用二次函数的性质求得OP=![]() 的最小值为
的最小值为![]() ,此时,求得b=﹣2a+3=
,此时,求得b=﹣2a+3=![]() ,R取得最小值为
,R取得最小值为![]() ﹣1,从而得到圆的标准方程.
﹣1,从而得到圆的标准方程.
解:(1)连接OQ,∵切点为Q,PQ⊥OQ,由勾股定理可得 PQ2=OP2﹣OQ2.
由已知PQ=PA,可得 PQ2=PA2,即 (a2+b2)﹣1=(a﹣2)2+(b﹣1)2.
化简可得 2a+b﹣3=0.
(2)∵PQ=![]() =
=![]() =
=![]() =
=![]() ,
,
故当a=![]() 时,线段PQ取得最小值为
时,线段PQ取得最小值为![]() .
.
(3)若以P为圆心所作的⊙P 的半径为R,由于⊙O的半径为1,∴|R﹣1|≤PO≤R+1.
而OP=![]() =
=![]() =
=![]() ,故当a=
,故当a=![]() 时,PO取得最小值为
时,PO取得最小值为![]() ,
,
此时,b=﹣2a+3=![]() ,R取得最小值为
,R取得最小值为![]() ﹣1.
﹣1.
故半径最小时⊙P 的方程为![]() +
+![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C所对的边分别是,a、b、c,△ABC的面积S= ![]()
![]()
![]() .
.
(Ⅰ)求A的大小;
(Ⅱ)若b+c=5,a= ![]() ,求△ABC的面积的大小.
,求△ABC的面积的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 分别是
分别是![]() 的边
的边![]() 的中点,连接
的中点,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠至
折叠至![]() 的位置,连接
的位置,连接![]() .记平面
.记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角大小.
所成锐二面角大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义两点A(xA , yA),B(xB , yB)间的“L﹣距离”为d(A﹣B)=|xA﹣xB|+|yA﹣yB|.现将边长为1的正三角形按如图所示方式放置,其中顶点A与坐标原点重合,记边AB所在的直线斜率为k(0≤k≤ ![]() ),则d(B﹣C)取得最大值时,边AB所在直线的斜率为 .
),则d(B﹣C)取得最大值时,边AB所在直线的斜率为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂抽取50名工人进行调查,发现他们一天加工零件的个数在50至350之间,现按生产的零件个数将他们分成六组,第一组[50,100),第二组[100,150),第三组[150,200),第四组[200,250),第五组[250,300),第六组[300,350],相应的样本频率分布直方图如图所示.
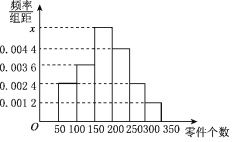
(1)求频率分布直方图中x的值;
(2)设位于第六组的工人为拔尖工,位于第五组的工人为熟练工,现用分层抽样的方法在这两类工人中抽取一个容量为6的样本,从样本中任意取两个,求至少有一个拔尖工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆内接四边形ABCD中,BD是圆的直径,AB=AC,延长AD与BC的延长线相交于点E,作EF⊥BD于F. 
(1)证明:EC=EF;
(2)如果DC= ![]() BD=3,试求DE的长.
BD=3,试求DE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com