
【题目】在平面直角坐标系中,定义两点A(xA , yA),B(xB , yB)间的“L﹣距离”为d(A﹣B)=|xA﹣xB|+|yA﹣yB|.现将边长为1的正三角形按如图所示方式放置,其中顶点A与坐标原点重合,记边AB所在的直线斜率为k(0≤k≤ ![]() ),则d(B﹣C)取得最大值时,边AB所在直线的斜率为 .
),则d(B﹣C)取得最大值时,边AB所在直线的斜率为 . 
【答案】2- ![]()
【解析】解:设B(cosθ,sinθ),则C(cos(θ+ ![]() ),sin(θ+
),sin(θ+ ![]() )),
)),
∴|BC|=|cos(θ+ ![]() )﹣cosθ|+|sin(θ+
)﹣cosθ|+|sin(θ+ ![]() )﹣sinθ|,
)﹣sinθ|,
∵0≤θ≤ ![]() ,
,
∴ ![]() ≤θ+
≤θ+ ![]() ≤
≤ ![]() <π,即0≤θ<θ+
<π,即0≤θ<θ+ ![]() <π,
<π,
∴|cos(θ+ ![]() )﹣cosθ|=cosθ﹣cos(θ+
)﹣cosθ|=cosθ﹣cos(θ+ ![]() ).
).
∵0≤θ≤ ![]() ,
, ![]() ≤θ+
≤θ+ ![]() ≤
≤ ![]() ,
,
∴|sin(θ+ ![]() )﹣sinθ|=sin(θ+
)﹣sinθ|=sin(θ+ ![]() )﹣sinθ,
)﹣sinθ,
|BC|=cosθ﹣cos(θ+ ![]() )+sin(θ+
)+sin(θ+ ![]() )﹣sinθ
)﹣sinθ
=cosθ﹣cosθcos ![]() +sinθsin
+sinθsin ![]() +sinθcos
+sinθcos ![]() +cosθsin
+cosθsin ![]() ﹣sinθ
﹣sinθ
= ![]() sinθ+
sinθ+ ![]() cosθ
cosθ
= ![]() sin(θ+φ)(tanφ=2+
sin(θ+φ)(tanφ=2+ ![]() ),
),
由θ+φ= ![]() 2kπ,k∈Z,得θ=﹣φ+
2kπ,k∈Z,得θ=﹣φ+ ![]() 2kπ,k∈Z,
2kπ,k∈Z,
∴tanθ=tan(﹣φ+ ![]() 2kπ)=
2kπ)= ![]() ,即边AB所在直线的斜率为2-
,即边AB所在直线的斜率为2- ![]() 时,则d(B﹣C)取得最大值,
时,则d(B﹣C)取得最大值,
所以答案是2- ![]() .
.
【考点精析】通过灵活运用直线的斜率,掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα即可以解答此题.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】某中学从参加环保知识竟赛的学生中抽取了部分学生的成绩进行分析,不过作好的茎叶图和频率分布直方图因故均受到不同程度的损坏,其可见部分信息如图所示,据此解答下列问题:

(1)求抽取学生成绩的中位数,并修复频率分布直方图;
(2)根据修复的频率分布直方图估计该中学此次环保知识竞赛的平均成绩。(以各组的区间中点值代表该组的各个值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上.
上.
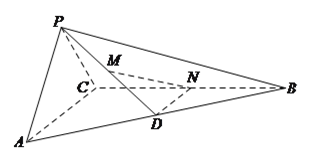
(![]() )当
)当![]() 为
为![]() 的中点时,证明:
的中点时,证明: ![]() 平面
平面![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )是否存在点
)是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且有|PQ|=|PA|.
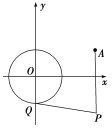
(1)求a,b间的关系;
(2)求|PQ|的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明天小强要参加班里组织的郊游活动,为了做好参加这次郊游的准备工作,他测算了如下数据:整理床铺、收拾携带物品8分钟,洗脸、刷牙7分钟,煮牛奶15分钟,吃早饭10分钟,查公交线路图9分钟,给出差在外的父亲发手机短信6分钟,走到公共汽车站10分钟,等公共汽车10分钟.小强粗略地算了一下,总共需要75分钟,为了赶上7:50的公共汽车,小强决定6:30起床,不幸的是他一下子睡到6:50,请你帮小强安排一下时间,画出一份郊游出行前时间安排流程图,使他还能来得及参加此次郊游.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,cosB= ![]() ,点D在线段BC上.
,点D在线段BC上. 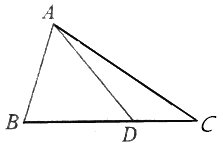
(1)若∠ADC= ![]() π,求AD的长;
π,求AD的长;
(2)若BD=2DC,△ACD的面积为 ![]()
![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com