
【题目】设有关于x的一元二次方程![]() =0.
=0.
(1)若a是从集合A={x∈Z|0≤x≤3}中任取一个元素,b是从集合B={x∈Z|0≤x≤2}中任取一个元素,求方程![]() =0恰有两个不相等实根的概率;
=0恰有两个不相等实根的概率;
(2) 若a是从集合A={x|0≤x≤3}中任取一个元素,b是从集合B={x|0≤x≤2}中任取一个元素,求上述方程有实根的概率.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)本题是古典概型,由分步计数原理知基本事件共12个,当a≥0,b≥0时,方程x2+2ax+b2=0有两个不相等实根的充要条件为a>b,满足条件的事件中包含6个基本事件,由古典概型公式得到结果;
(2)本题是几何概型,试验的全部约束所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.构成事件B的区域为{(a,b)|0≤a≤3,0≤b≤2,a>b},画出图形,求出对应面积,由面积比得答案.
(1)由题意知a取集合{0,1,2,3}中任一个元素,b取集合{0,1,2}中任一个元素,a,b取值的所有情况是:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个数表示a的取值,第二个数表示b的取值,即基本事件总数为12. 记“方程![]() 恰有两个不相等的实根”为事件A, 其等价于a>b. 而当a>b时,a,b取值的情况有(1,0), (2,0),(2,1), (3,0),(3,1),(3,2),即A包含的基本事件数为6,所以方程
恰有两个不相等的实根”为事件A, 其等价于a>b. 而当a>b时,a,b取值的情况有(1,0), (2,0),(2,1), (3,0),(3,1),(3,2),即A包含的基本事件数为6,所以方程![]() 恰有两个不相等实根的概率P(A)=
恰有两个不相等实根的概率P(A)=![]() =
=![]() .
.
(2)设事件B为“方程![]() 有实根”.当a≥0,b≥0时,方程
有实根”.当a≥0,b≥0时,方程![]() 有实根需满足a≥b.试验的全部结束所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.构成事件B的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}(如下图所示的阴影部分).
有实根需满足a≥b.试验的全部结束所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.构成事件B的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}(如下图所示的阴影部分).
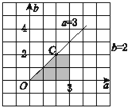
因此所求的概率为P(B)=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 分别是
分别是![]() 的边
的边![]() 的中点,连接
的中点,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠至
折叠至![]() 的位置,连接
的位置,连接![]() .记平面
.记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角大小.
所成锐二面角大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若![]() ,
, ![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑤设![]() ,则函数
,则函数![]() 的最小值是
的最小值是![]() ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
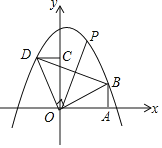
【题目】如图所示,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到![]() ,抛物线
,抛物线![]() 经过B、D两点.
经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后抛掷两枚骰子,设出现的点数之和是12,11,10的概率依次是P1,P2,P3,则( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数对(x,y),设映射f:(x,y)→( ![]() ,
, ![]() ),并定义|(x,y)|=
),并定义|(x,y)|= ![]() ,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
A.4 ![]()
B.8 ![]()
C.16 ![]()
D.32 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定集合A={a1 , a2 , a3 , …,an}(n∈N* , n≥3)中,定义ai+aj(1≤i<j≤n,i,j∈N*)中所有不同值的个数为集合A两元素和的容量,用L(A)表示.若数列{an}是公差不为0的等差数列,设集合A={a1 , a2 , a3 , …,a2016},则L(A)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com