
| A.P∧Q为真 | B.¬P∨Q为真 | C.P∧¬Q为真 | D.¬P∧¬Q为真 |
科目:高中数学 来源: 题型:
(08年黄冈中学二模文)甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为![]() ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为![]() ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为![]() .每人闯关成功记2分,三人得分之和记为小组团体总分.
.每人闯关成功记2分,三人得分之和记为小组团体总分.
(I)求乙、丙各自闯关成功的概率;
(II)求团体总分为4分的概率;
(III)若团体总分不小于4分,则小组可参加复赛.求该小组参加复赛的概率.
查看答案和解析>>
科目:高中数学 来源:东城区模拟 题型:填空题
| x |
| 1+|x| |
查看答案和解析>>
科目:高中数学 来源:怀化一模 题型:单选题
| 1 |
| 2 |
| A.(-∞,-1) | B.(-1,3) | C.(-3,+∞) | D.(-3,1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
|
|
|
| A.②③ | B.①②③ | C.②④ | D.①②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
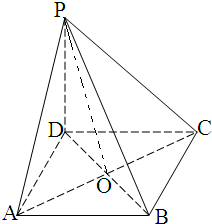
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:安徽省模拟题 题型:填空题
 (t为参数),则它的倾斜角为
(t为参数),则它的倾斜角为 ;
; 查看答案和解析>>
科目:高中数学 来源: 题型:
(08年黄冈中学二模文)某学校共在2008名学生,将从中选项派5名学生在某天去国家大剧院参加音乐晚会,若采用以下方法选取:先用简单随机抽样从2008名学生中剔除8名学生,再从2000名学生中随机抽取5名,则其中学生甲被选取的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com