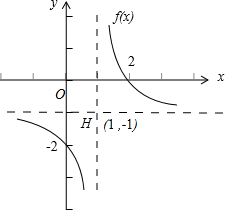
解:(1)函数
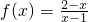
=-
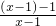
=-1+

,故把函数y=

的图象向右平移1个单位,
再向下平移1个单位,即可得到函数f(x)的图象,如图所示:
(2)函数f(x)的减区间为(-∞,1)、(1,+∞).
函数f(x)在区间(-3,1)上是减函数,在(1,+∞)上是减函数.
证明:设-3<x
1<x
2<1,则f(x
1)-f(x
2)=
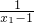
-
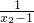
=

.
由题设可得 x
2-x
1>0,x
1-1<0,x
2-1<0,∴

>0,
故有f(x
1)-f(x
2)>0,f(x
1)>f(x
2),故函数f(x)在区间(-3,1)上是减函数.
同理可证,函数f(x)在在(1,+∞)上是减函数.
(3)函数f(x)-g(x)的零点个数,即函数f(x)和函数g(x)=(x+1)
3 的图象交点的个数,
在同一个坐标系中,画出函数函数f(x)和函数g(x)=(x+1)
3 的图象,如图所示,
由于这2个函数的图象仅有2个交点,故函数f(x)-g(x)的零点个数为2.

分析:(1)化简函数解析式为
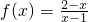
-1+

,故把函数y=

的图象向右平移1个单位,再向下平移1个单位,即可得到函数f(x)的图象,如图所示.
(2)函数f(x)的减区间为(-∞,1)、(1,+∞),用函数的单调性的定义证明函数f(x)在区间(-3,1)上是减函数,在(1,+∞)上是减函数.
(3)函数f(x)-g(x)的零点个数,即函数f(x)和函数g(x)=(x+1)
3 的图象交点的个数,在同一个坐标系中,画出函数函数f(x)和函数g(x)=
(x+1)
3 的图象,数形结合可得由于这2个函数的图象仅有2个交点,从而得出结论.
点评:本题主要考查函数的单调性的判断和证明,函数的图象特征,函数的零点与方程根的关系,体现了数形结合的数学思想,属于中档题.

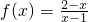 ,g(x)=(x+1)3
,g(x)=(x+1)3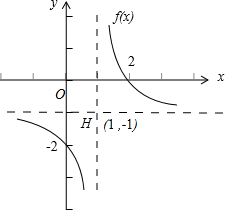 解:(1)函数
解:(1)函数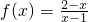 =-
=-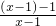 =-1+
=-1+ ,故把函数y=
,故把函数y= 的图象向右平移1个单位,
的图象向右平移1个单位,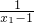 -
-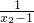 =
= .
. >0,
>0,
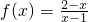 -1+
-1+ ,故把函数y=
,故把函数y= 的图象向右平移1个单位,再向下平移1个单位,即可得到函数f(x)的图象,如图所示.
的图象向右平移1个单位,再向下平移1个单位,即可得到函数f(x)的图象,如图所示.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案