
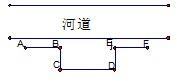
 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求科目:高中数学 来源:2007届中山二中数学(文科)模拟试题 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
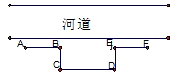 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三一轮复习质量检测理科数学 题型:解答题
(12分) 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
(1)y关于x的函数解析式y=f(x);
(2)若BC的长不得超过40m,则当BC为何值时,y有最 小值,并求出这个最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
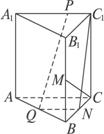
(1)若P是A![]() ;
;
(2)求二面角A-A1B-C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com