
分析 ①,$a=4,c=2,e=\frac{1}{2}$,即可判断出正误.
②,若焦点在x轴上,则$\frac{{\sqrt{12-m}}}{{\sqrt{12}}}=\frac{{\sqrt{5}-1}}{2}$,解得m.若焦点在y轴上,则$\frac{{\sqrt{m-12}}}{{\sqrt{m}}}=\frac{{\sqrt{5}-1}}{2}$,解得m,即可判断出正误.
③,c=2,$\frac{c}{a}=\frac{{\sqrt{5}-1}}{2}$,即可判断出正误.
④,$|{AB}|=\frac{{2{b^2}}}{a}=\frac{{2({{a^2}-{c^2}})}}{a}=({\sqrt{5}-1})a$,即可判断出正误.
⑤,设|PF1|=m,|PF2|=n,则$\left\{\begin{array}{l}m+n=2a\\ 4{c^2}={m^2}+{n^2}\end{array}\right.,mn=2{a^2}-2{c^2}$,而$\frac{{\sqrt{5}-1}}{2}=\frac{c}{a}$,可得mn,与m+n=2a联立即可判断出正误.
解答 解:对①,$a=4,c=2,e=\frac{1}{2}$,①不正确.
对②,若焦点在x轴上,则$\frac{{\sqrt{12-m}}}{{\sqrt{12}}}=\frac{{\sqrt{5}-1}}{2}$,解得$m=6\sqrt{5}-6$.若焦点在y轴上,则$\frac{{\sqrt{m-12}}}{{\sqrt{m}}}=\frac{{\sqrt{5}-1}}{2}$,解得$m=6\sqrt{5}+6$,②不正确.
对③,c=2,$\frac{c}{a}=\frac{{\sqrt{5}-1}}{2}$,$2a+2c=6+2\sqrt{5}$,③正确.
对④,$|{AB}|=\frac{{2{b^2}}}{a}=\frac{{2({{a^2}-{c^2}})}}{a}=({\sqrt{5}-1})a$,④正确.
对⑤,设|PF1|=m,|PF2|=n,则$\left\{\begin{array}{l}m+n=2a\\ 4{c^2}={m^2}+{n^2}\end{array}\right.,mn=2{a^2}-2{c^2}$,而$\frac{{\sqrt{5}-1}}{2}=\frac{c}{a}$,∴$mn=2{a^2}-2{({\frac{{\sqrt{5}-1}}{2}a})^2}=({\sqrt{5}-1}){a^2}$,与m+n=2a联立无实数解.因此椭圆E上满足∠F1PF2=90°的点P不存在,⑤正确.
故答案为:③④⑤.
点评 本题考查了椭圆的标准方程及其性质,考查学生运算能力、综合运用知识和方法解决问题的能力,属于中档题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{1}{10}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
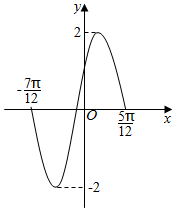 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则下列判断错误的是( )| A. | A=2 | B. | ω=2 | C. | f(0)=1 | D. | φ=$\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | B. | $({\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ | C. | $({-\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | D. | $({-\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
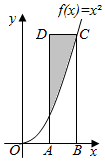 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{7}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com