
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设f(x)为奇函数, 且在(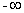 , 0)内是减函数, f(3)= 0,则x f(x)<0的解集为( )
, 0)内是减函数, f(3)= 0,则x f(x)<0的解集为( )
A. (-3, 0)∪(3, +∞) B. (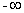 , -3)∪(0, 3 )
, -3)∪(0, 3 )
C. (-3, 0)∪(0, 3 ) D. (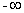 , -3)∪(3, +∞)
, -3)∪(3, +∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
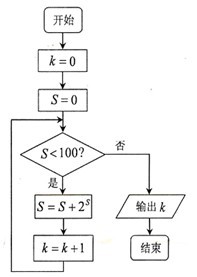
某程序框图如右图所示,该程序运行后输出的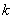 的值是 ( )
的值是 ( )
A. B.
B.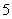 C.
C.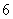 D.
D. 12若
12若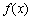 是定义在
是定义在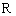 上的函数,对任意的实数
上的函数,对任意的实数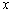 ,都有
,都有 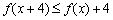 和
和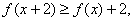 且
且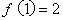 ,则
,则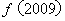 的值是( )
的值是( )
A.2008 B.2009 C.2010 D.2011.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的相邻两项an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,且a1=1.
(1)求数列{ an}和{bn}的通项公式;
(2)设Sn是数列{an}的前n项的和,问是否存在常数λ,使得bn-λSn>0对任意n∈N*都成立,若存在,求出λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
某班有48名学生,其中男生32人,女生16人,李老师随机地抽查8名学生的作业,用X表示抽查到的女生人数,则E(X)的值为( )
A.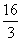 B.
B.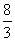 C.3 D.4
C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的相邻两项an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,且a1=1.
(1)求数列{ an}和{bn}的通项公式;
(2)设Sn是数列{an}的前n项的和,问是否存在常数λ,使得bn-λSn>0对任意n∈N*都成立,若存在,求出λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题为真命题的序号是
是两个不同的平面,下列命题为真命题的序号是
①若 ,则
,则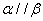 ;
;
②若 ,则
,则 ;
;
③若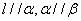 ,则
,则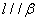 ;
;
④若 ,则
,则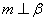 .
.
A.①④ B.①③ C.②④ D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com