Question

9．已知函数f（x）=$\frac{1}{2}$x²-2x-3lnx，g（x）=$\frac{1}{2}$x²-3x-$\frac{1}{2}$a（a∈R）．
（1）若?x＞0，f（x）≥m恒成立，求实数m的取值范围；
（2）设函数F（x）=f（x）-2g（x），若F（x）在[1，5]上有零点，求实数a的取值范围．

Answer 1

分析 （1）?x＞0，f（x）≥m恒成立，∴m≤[f（x）]_min，利用导数研究其单调性极小值与最小值即可得出．
（2）函数F（x）=f（x）-2g（x）在[1，5]上有零点，等价于方程f（x）-2g（x）=0在[1，5]上有解．化为$\frac{1}{2}{x^2}-4x+3lnx=a$．设$h（x）=\frac{1}{2}{x^2}-4x+3lnx$．利用导数研究其单调性极值与最值，可得函数h（x）在[1，5]上值域即可得出．

解答 解：（1）由题意得f（x）的定义域为（0，+∞），
$f'（x）=x-2-\frac{3}{x}=\frac{{{x^2}-2x-3}}{x}=\frac{（x+1）（x-3）}{x}$．
∵x＞0，∴f'（x）、f（x）随x的变化情况如下表：

x	（0，3）	3	（3，+∞）
f'（x）	-	0	+
f（x）	单调递减	极小值	单调递增

由表格可知：$f{（x）_{min}}=f（3）=-\frac{3}{2}-3ln3$．
∵f（x）≥m在（0，+∞）上恒成立，∴$m≤-\frac{3}{2}-3ln3$．
（2）函数F（x）=f（x）-2g（x）在[1，5]上有零点，
等价于方程f（x）-2g（x）=0在[1，5]上有解．
化简，得$\frac{1}{2}{x^2}-4x+3lnx=a$．
设$h（x）=\frac{1}{2}{x^2}-4x+3lnx$．
则$h'（x）=x-4+\frac{3}{x}=\frac{（x-1）（x-3）}{x}$，∵x＞0，∴h'（x）、h（x）随x的变化情况如下表：

x	（0，1）	1	（1，3）	3	（3，+∞）
h'（x）	+	0	-	0	+
h（x）	单调递增	$-\frac{7}{2}$	单调递减	$3ln3-\frac{15}{2}$	单调递增

且$h（1）=-\frac{7}{2}$，$h（3）=3ln3-\frac{15}{2}$，$h（5）=3ln5-\frac{15}{2}$，
h（5）-h（1）=3ln5-4=ln5³-lne⁴＞0．
作出h（x）在[1，5]上的大致图象（如图所示）．
∴当$3ln3-\frac{15}{2}≤a≤3ln5-\frac{15}{2}$时，
$\frac{1}{2}{x^2}-4x+3lnx=a$在[1，5]上有解．
故实数a的取值范围是$[3ln3-\frac{15}{2}，3ln5-\frac{15}{2}]$．

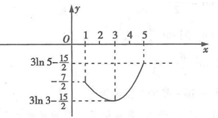
点评 本题考查了利用导数研究函数的单调性极值与最值、等价转化方法、不等式的解法、函数的值域与零点，考查了分析问题与解决问题的能力、数形结合方法、推理能力与计算能力，属于难题．