练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．某班甲、乙两名学生的高考备考成绩的茎叶图如图所示，分别求两名学生成绩的中位数和平均分．

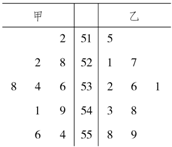
    分析 根据茎叶图中的数据，利用中位数与平均数的定义进行计算即可．

    解答 解：将甲、乙两学生的成绩从小到大排列为：
    甲：512　522 　528　534　536　538　541　549　554　556
    乙：515　521　527　531　532　536　543　548　558　559
    从以上排列可知甲学生成绩的中位数为$\frac{536+538}{2}$=537，
    乙学生成绩的中位数为$\frac{532+536}{2}$=534；
    甲学生成绩的平均分为
    500+$\frac{12+22+28+34+36+38+41+49+54+56}{10}$=537，
    乙学生成绩的平均分为
    500+$\frac{15+21+27+31+32+36+43+48+58+59}{10}$=537．

    点评 本题考查了利用茎叶图中的数据计算中位数与平均数的问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=2x-$\frac{b}{x}$，（b＞0），证明：f（x）在（0，+∞）上单调递增．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知x＞0，y＞0，且x+2y=xy，若x+2y＞m2+2m恒成立，则xy的最小值为8，实数m的取值范围为（-4，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知集合A={x|x2-4x+3≤0}，B={2，3，4}，则A∩B=（　　）
    A．{2}B．{2，3}C．{3}D．{2，3，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．方程2x+3x+5x=7x共有（　　）个不同的实根．
    A．0B．1C．2D．无数多个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．（1）计算：27${\;}^{\frac{2}{3}}}$+16${\;}^{-\;\;\frac{1}{2}}}$-（$\frac{1}{2}$）-2-（$\frac{8}{27}$）${\;}^{-\frac{2}{3}}}$；
    （2 ） 化简：（${\sqrt{a-1}}$）2+$\sqrt{{{（1-a）}^2}}$+$\root{3}{{{{（1-a）}^3}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=x3-3ax2+3bx的图象与直线12x+y-1=0相切于点（1，-11）．
    （1）求a，b的值；
    （2）求函数f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在平面区域M={（x，y）|$\left\{\begin{array}{l}{y≥x}\\{x≥0}\\{x+y≤2}\end{array}\right.$}内随机取一点P，则点P在圆x2+y2=2内部的概率（　　）
    A．$\frac{π}{8}$B．$\frac{π}{4}$C．$\frac{π}{2}$D．$\frac{3π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设集合A={y|y=x2-2x+1，0≤x≤3}，集合B={x|x2-（2m-1）x+m（m-1）≤0}．已知命题p：x∈A，命题q：x∈B，且命题p是命题q的必要不充分条件，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案