
分析 (1)由${S_n}={n^2}{a_n}-n({n-1})$(n≥2)得:${S_n}={n^2}({S_n}-{S_{n-1}})-n({n-1})$,可得$\frac{n+1}{n}{S_n}-\frac{n}{n-1}{S_{n-1}}=1$,对n≥2成立.
(2)利用“累加求和”方法即可得出.
解答 解:(1)由${S_n}={n^2}{a_n}-n({n-1})$(n≥2)得:${S_n}={n^2}({S_n}-{S_{n-1}})-n({n-1})$,即$({n^2}-1){S_n}-{n^2}{S_{n-1}}=n({n-1})$,
所以$\frac{n+1}{n}{S_n}-\frac{n}{n-1}{S_{n-1}}=1$,对n≥2成立.
由递推公式可先得出${s_1}=\frac{1}{2},{s_2}=\frac{4}{3},{s_3}=\frac{9}{4}$;
(2)猜测${S_n}=\frac{n^2}{n+1}$,
由$\frac{n+1}{n}{S_n}-\frac{n}{n-1}{S_{n-1}}=1$,$\frac{n}{n-1}{S_{n-1}}-\frac{n-1}{n-2}{S_{n-2}}=1$,…,$\frac{3}{2}{S_2}-\frac{2}{1}{S_1}=1$,
相加得:$\frac{n+1}{n}{S_n}-2{S_1}=n-1$,又${S_1}={a_1}=\frac{1}{2}$,
所以${S_n}=\frac{n^2}{n+1}$,当n=1时,也成立.
点评 本题考查了数列递推关系、“累加求和”方法,考查了推理能力与计算能力,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 10 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m>0,则x2+x-m=0没有实根 | B. | 若m<0,则x2+x-m=0没有实根 | ||
| C. | 若m≤0,则x2+x-m=0有实根 | D. | 若m≤0,则x2+x-m=0没有实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,4) | B. | (-1,3] | C. | [-2,-1] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
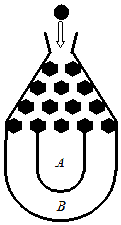 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com