
分析 (1)先任取x1<x2,x2-x1>0.由当x>0时,f(x)>3.得到f(x2-x1)>3,再对f(x2)按照f(a+b)=f(a)+f(b)-3变形得到结论;
(2)由f(4)=2,再将f(3m2-m-2)>$\frac{5}{2}$转化为f(3m2-m-2)>f(2),由(1)中的结论,利用单调性求解.
解答 解:(1)证明:任取x1<x2,
∴x2-x1>0,
∴f(x2-x1)>3.
∴f(x2)=f[x1+(x2-x1)]=f(x1)+f(x2-x1)-3>f(x1),
∴f(x)是R上的增函数;
(2)∵f(4)=f(2)+f(2)-3=2,可得f(2)=$\frac{5}{2}$,
∴f(3m2-m-2)>$\frac{5}{2}$=f(2),
又由(1)的结论知,f(x)是R上的增函数,
∴3m2-m-2>2,
3m2-m-4>0,
∴m<-1或m>$\frac{4}{3}$,
即不等式的解集为{m|m<-1或m>$\frac{4}{3}$}.
点评 本题主要考查抽象函数的单调性证明和利用单调性定义解抽象不等式,利用定义法以及转化法是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 估计准确与否值与所分组数有关 | B. | 样本容量越大,估计结果越准确 | ||
| C. | 估计准确与否值域总体容量有关 | D. | 估计准确与否与样本容量无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 503 | B. | $\frac{1007}{2}$ | C. | 1006 | D. | 1007 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
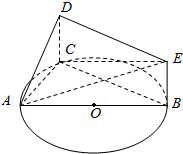 如图,AB是圆O的直径,C是圆O上异于A、B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A、B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com