解:对于①又∵1°当-1≤x≤1时,-1≤-x≤1,
∴g(-x)=0.
又g(x)=0,∴g(-x)=g(x).
2°当x<-1时,-x>1,
∴g(-x)=-(-x)+2=x+2.
又∵g(x)=x+2,∴g(-x)=g(x).
3°当x>1时,-x<-1,
∴g(-x)=(-x)+2=-x+2.
又∵g(x)=-x+2,∴g(-x)=g(x).
综上,对任意x∈R都有g(-x)=g(x).
∴g(x)为偶函数.正确;

②将x=

代入到函数f(x)中得到f(

)=3sin(2×

-

)=0
函数f(x)=3sin(2x-

)的图象关于点(

,0)对称,故②正确;
③若m=0不成立,故错;
④由y=3Sin2x的图象向右平移

个单位长度可以得到图象f(x)=3sin[2(x-

)-

].即f(x)=3sin(2x-

).
故正确.
故答案为:①②④.
分析:对于①g(x)判断时,要注意从三种情况判断,即从1°当-1≤x≤1时2°当x<-1时3°当x>1时判断.
对于②,将x=

代入到函数f(x)得到f(

)=0,进而可知它是对称中心,②正确;
对于③,若m=0不成立;
对于④,根据左加右减的原则进行平移可知将y=3sin2x的图象左平移

得到得图象是函数
f(x),故④正确.
点评:本题主要考查了正弦函数的对称性、单调性,以及函数y=Asin(ωx+φ)的图象变换,属于基础题.考查正弦函数的基本性质--对称性、单调性的应用和三角函数的平移,三角函数的平移的原则是左加右减,上加下减.还考查函数奇偶性的判断,要注意分段函数的判断,分几段就从几个方面判断.

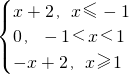 为偶函数;②函数f(x)=3sin(2x-
为偶函数;②函数f(x)=3sin(2x- )的图象关于点(
)的图象关于点( ,0)对称;
,0)对称; =m
=m (m∈R),则有
(m∈R),则有 =
=
 个单位长度可以得到图象f(x)=3sin(2x-
个单位长度可以得到图象f(x)=3sin(2x- ).
).
 代入到函数f(x)中得到f(
代入到函数f(x)中得到f(  )=3sin(2×
)=3sin(2× -
- )=0
)=0 )的图象关于点(
)的图象关于点( ,0)对称,故②正确;
,0)对称,故②正确; 个单位长度可以得到图象f(x)=3sin[2(x-
个单位长度可以得到图象f(x)=3sin[2(x- )-
)- ].即f(x)=3sin(2x-
].即f(x)=3sin(2x- ).
). 代入到函数f(x)得到f(
代入到函数f(x)得到f(  )=0,进而可知它是对称中心,②正确;
)=0,进而可知它是对称中心,②正确; 得到得图象是函数
得到得图象是函数

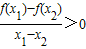 ,给出如下命题:
,给出如下命题: