
已知某圆的极坐标方程是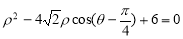 ,求:
,求:
(1)求圆的普通方程和一个参数方程;
(2)圆上所有点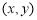 中
中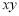 的最大值和最小值.
的最大值和最小值.
(1)即圆的普通方程为: 。 参数方程为:
。 参数方程为:  (
(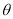 为参数) ;(2)最大值为:9,最小值为:1.
为参数) ;(2)最大值为:9,最小值为:1.
【解析】
试题分析:(1)圆的普通方程与圆的极坐标方程之间的转换关系在于圆上一点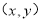 与极径
与极径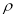 ,极角
,极角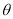 间的关系:
间的关系: ,圆的普通方程与圆的参数方程的关系也在于此,即圆上一点
,圆的普通方程与圆的参数方程的关系也在于此,即圆上一点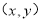 与圆半径
与圆半径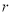 ,圆上点与圆心
,圆上点与圆心 连线与
连线与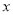 轴正向夹角
轴正向夹角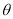 的关系:
的关系: ;(2)利用圆的参数方程,将
;(2)利用圆的参数方程,将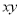 转化为关于
转化为关于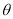 的三角函数关系求最值,注意这里处理要注意用换元法(不同于一般三角函数处理方法,即转化为
的三角函数关系求最值,注意这里处理要注意用换元法(不同于一般三角函数处理方法,即转化为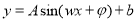 的形式),得到三角函数与二次函数的复合函数.
的形式),得到三角函数与二次函数的复合函数.
试题解析:
由圆上一点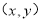 与极径
与极径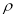 ,极角
,极角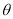 间的关系:
间的关系: ,
,
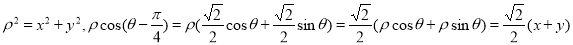 ,
,
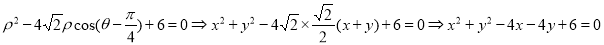
即圆的普通方程为: 。 2分
。 2分
可得圆心坐标为 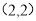 ,半径
,半径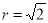
所以其参数方程为:  (
(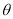 为参数) 。 4分
为参数) 。 4分
由圆上一点与圆的参数方程的关系得:
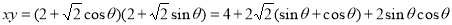 5分
5分
令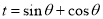 ,
,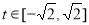 , 则
, 则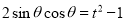 .
.
所以  6分
6分
当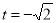 时,最小值是1; 8分
时,最小值是1; 8分
当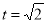 时,最大值是9. 10分
时,最大值是9. 10分
考点:(1)圆的极坐标方程与圆的参数方程;(2)参数方程求最值应用。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源:2015届重庆一中高二下学期期中考试文科数学试卷(解析版) 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量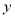 (单位:千克)与销售价格
(单位:千克)与销售价格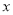 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式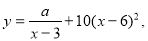 其中
其中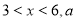 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求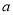 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格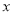 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设随机变量X服从正态分布N(0,1),P(X>1)=p,则P(-1<X<0)等于
A.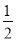 p B.1-p C.1-2p D.
p B.1-p C.1-2p D.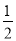 -p
-p
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知随机变量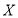 服从正态分布
服从正态分布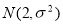 ,
,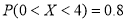 ,则
,则 的值等于( )
的值等于( )
A.0.1 B.0.2 C.0.4 D.0.6
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
某汽车销售公司在A、B两地销售同一种品牌的汽车,在A地的销售利润(单位:万元)为y1=4.1x-0.1x2,在B地的销售利润(单位:万元)为y2=2x,其中x为销售量(单位:辆).若该公司在两地共销售16辆这种品牌汽车,则能获得的最大利润是( )
A.10.5万元 B.11万元 C.43万元 D.43.025万元
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:填空题
古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···,第n个三角形数为 。记第n个k边形数为N(n,k)(
。记第n个k边形数为N(n,k)(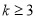 ),以下列出了部分k边形数中第n个数的表达式:
),以下列出了部分k边形数中第n个数的表达式:
三角形数 N(n,3)=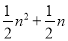
正方形数 N(n,4)=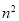
五边形数 N(n,5)=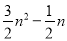
六边形数 N(n,6)=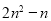
可以推测N(n,k)的表达式,由此计算N(10,24)= ____________
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试文科数学试卷(解析版) 题型:解答题
在四棱锥 中,底面
中,底面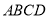 为矩形,
为矩形,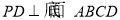 ,
,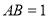 ,
,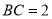 ,
, ,
,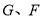 分别为
分别为 的中点.
的中点.
(1) 求证: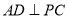 ;
;
(2) 求证: 平面
平面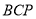 ;
;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com