
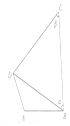
 如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).
如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$). 分析 由正弦定理,三角形内角和定理,两角和的正弦函数公式化简已知等式可得$\sqrt{3}$cosβsinα=sinαsinβ,进而可求tan$β=\sqrt{3}$,结合范围β∈(0,π),可求$β=\frac{π}{3}$,根据题意,∠BAD=$\frac{2π}{3}$,由余弦定理,基本不等式可求CB+CD≤2$\sqrt{7}$,利用两边之和大于第三边可求CB+CD>$\sqrt{7}$,即可得解四边形ABCD的周长的取值范围.
解答 解:∵$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,
∴$\sqrt{3}$sin∠BDC=$\sqrt{3}$sinβcosα+sinαsinβ,
∴$\sqrt{3}$sin(α+β)=$\sqrt{3}$sinβcosα+sinαsinβ,
∴$\sqrt{3}$(cosβsinα+cosαsinβ)=$\sqrt{3}$sinβcosα+sinαsinβ,
∴$\sqrt{3}$cosβsinα=sinαsinβ,
∴tan$β=\sqrt{3}$,
又∵β∈(0,π),
∴$β=\frac{π}{3}$,
根据题意,∠BAD=$\frac{2π}{3}$,由余弦定理,BD2=AB2+AD2-2AB•ADcos∠BAD=4+1-2×2×1×cos$\frac{2π}{3}$=7,
又∵BD2=CB2+CD2-2CB•CDcosβ=(CB+CD)2-3CB•CD≥(CB+CD)2-$\frac{3(CB+CD)^{2}}{4}$=$\frac{(CB+CD)^{2}}{4}$,
∴CB+CD≤2$\sqrt{7}$,
又∵CB+CD>$\sqrt{7}$,
∴四边形ABCD的周长AB+CB+CD+DA的取值范围为:(3+$\sqrt{7}$,3+2$\sqrt{7}$).
故答案为:(3+$\sqrt{7}$,3+2$\sqrt{7}$).
点评 本题主要考查了正弦定理,余弦定理的应用和解三角形的基本知识以及运算求解能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
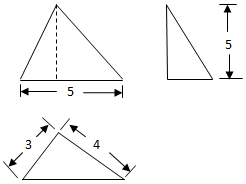
| A. | $4\sqrt{2}$ | B. | $\sqrt{34}$ | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 无解 | B. | 有一解 | C. | 有两解 | D. | 有无数解 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{e^π}(1-{e^{2017π}})}}{{1-{e^{2π}}}}$ | B. | $\frac{{{e^π}(1-{e^{1009π}})}}{{1-{e^π}}}$ | ||
| C. | $\frac{{{e^π}(1-{e^{1008π}})}}{{1-{e^{2π}}}}$ | D. | $\frac{{{e^π}(1-{e^{2016π}})}}{{1-{e^{2π}}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com