
分析 (1)利用x2的系数为180得到关于n的方程解之;
(2)利用赋值法,将x分别赋值为1和-1,得到各项系数关系,对所求分解因式求值;
(3)将m,n代入,求出ak,分析S表达式,得到即$\frac{1}{{C_{2016}^k}}=\frac{2017}{2018}(\frac{1}{{C_{2017}^k}}+\frac{1}{{C_{2017}^{k+1}}})$,k=0,1,2,…,2016. 从而累加求和.
解答 解:(1)当m=2时,${a_2}=C_n^2×{2^2}=180$,即$\frac{n(n-1)}{2}=45$,解得n=10或n=-9(舍),
所以n的值为10. …(4分)
(2)当$m=\sqrt{2}$,n=8时,
令x=1,则${(1+\sqrt{2})^8}={a_0}+{a_1}+{a_2}+{a_3}+{a_4}+{a_5}+{a_6}+{a_7}+{a_8}$,
令x=-1,则${(1-\sqrt{2})^8}={a_0}-{a_1}+{a_2}-{a_3}+{a_4}-{a_5}+{a_6}-{a_7}+{a_8}$,
所以${({a_0}+{a_2}+{a_4}+{a_6}+{a_8})^2}-{({a_1}+{a_3}+{a_5}+{a_7})^2}={(1+\sqrt{2})^8}{(1-\sqrt{2})^8}=1$.…(8分)
(3)当m=-1,n=2016时,${(1-x)^n}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_n}{x^n}$,
则${a_k}=C_{2016}^k{(-1)^k}$,k=0,1,2,…,2016,
所以$S=\frac{1}{{C_{2016}^0}}-\frac{1}{{C_{2016}^1}}+\frac{1}{{C_{2016}^2}}-\frac{1}{{C_{2016}^3}}+…-\frac{1}{{C_{2016}^{2015}}}+\frac{1}{{C_{2016}^{2016}}}$. …(10分)
考虑$\frac{1}{{C_{2017}^k}}+\frac{1}{{C_{2017}^{k+1}}}=\frac{k!(2017-k)!}{2017!}+\frac{(k+1)!(2016-k)!}{2017!}$=$\frac{k!(2016-k)!×2018}{2017!}$=$\frac{2018}{2017}×\frac{1}{{C_{2016}^k}}$,
即$\frac{1}{{C_{2016}^k}}=\frac{2017}{2018}(\frac{1}{{C_{2017}^k}}+\frac{1}{{C_{2017}^{k+1}}})$,k=0,1,2,…,2016. …(14分)
所以$S=\frac{2017}{2018}[(\frac{1}{{C_{2017}^0}}+\frac{1}{{C_{2017}^1}})-(\frac{1}{{C_{2017}^1}}+\frac{1}{{C_{2017}^2}})+(\frac{1}{{C_{2017}^2}}+\frac{1}{{C_{2017}^3}})-…$$-(\frac{1}{{C_{2017}^{2015}}}+\frac{1}{{C_{2017}^{2016}}})+(\frac{1}{{C_{2017}^{2016}}}+\frac{1}{{C_{2017}^{2017}}})]$=$\frac{2017}{2018}(\frac{1}{{C_{2017}^0}}+\frac{1}{{C_{2017}^{2017}}})=\frac{2017}{1009}$.
故$S=\sum_{k=0}^{2016}{\frac{1}{a_k}}$的值为$\frac{2017}{1009}$. …(16分)
点评 本题考查了二项展开式中,项的系数问题;主要用到了赋值法的思想解答.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
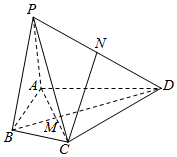 如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.
如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com