
分析 (Ⅰ)消去参数求曲线E的普通方程,利用过P(2,0)作倾斜角为α得到l的参数方程;
(Ⅱ)将l的参数方程代入E,利用判别式大于等于0求sinα的取值范围
解答 解:(Ⅰ)曲线E$\left\{\begin{array}{l}{x=cosθ}\\{y=\frac{\sqrt{2}}{2}sinθ}\end{array}\right.$(θ为参数),曲线E的普通方程为x2+2y2=1;
过P(2,0)作倾斜角为α的直线l的参数方程为$\left\{\begin{array}{l}{x=2+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数);
(Ⅱ)将l的参数方程代入E,可得(1+sin2α)t2+(4cosα)t+3=0,
△=(4cosα)2-4(1+sin2α))×3≥0,
∴sin2α≤$\frac{1}{7}$,
∴sinα的取值范围是0≤sinα≤$\frac{\sqrt{7}}{7}$.
点评 本题考查参数方程,考查参数方程化为普通方程,考查学生的计算能力.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {k|0<k≤1} | B. | {k|k<0或k>1} | C. | {k|0≤k≤1} | D. | {k|k>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
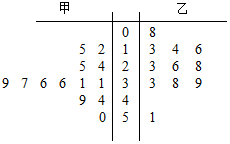 某赛季甲,乙两名篮球运动员每场比赛得分可用茎叶图表示如下:
某赛季甲,乙两名篮球运动员每场比赛得分可用茎叶图表示如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,A为圆O外一点,AO与圆交于B,C两点,AB=4,AD为圆O的切线,D为切点,AD=8,∠BDC的角平分线与BC和圆O分别交于E,F两点.
如图所示,A为圆O外一点,AO与圆交于B,C两点,AB=4,AD为圆O的切线,D为切点,AD=8,∠BDC的角平分线与BC和圆O分别交于E,F两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com