
(本题12分)
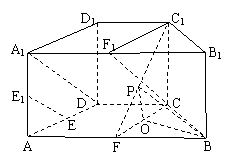 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA![]() =2, E、E
=2, E、E![]() 、F分别是棱AD、AA
、F分别是棱AD、AA![]() 、AB的中点。
、AB的中点。
(I)证明:直线EE![]() //平面FCC
//平面FCC![]() ;
;
(II)求二面角B-FC![]() -C的余弦值。
-C的余弦值。
(本小题满分12分)
解:(1)因为AB=4, BC=CD=2, F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
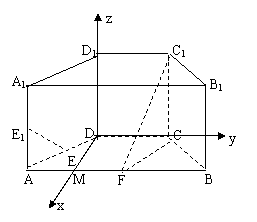 等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为
z轴建立空间直角坐标系,… …………… ………1分
,则D(0,0,0),A(![]() ,-1,0),F(
,-1,0),F(![]() ,1,0),C(0,2,0),
,1,0),C(0,2,0),
C1(0,2,2),E(![]() ,
,![]() ,0),E1(
,0),E1(![]() ,-1,1), ………… …… ………2分
,-1,1), ………… …… ………2分
所以![]() ,
,![]() ,
,![]()
![]() 设平面CC1F的法向量为
设平面CC1F的法向量为![]() 则
则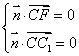 所以
所以
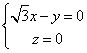 取
取![]() , …… ……………4分
, …… ……………4分
则![]() ,所以
,所以![]() ,
,
所以直线EE![]() //平面FCC
//平面FCC![]() . ………… …………… …… …………………6分
. ………… …………… …… …………………6分
(2)![]() ,设平面BFC1的法向量为
,设平面BFC1的法向量为![]() ,则
,则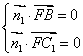 所以
所以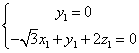 ,取
,取![]() ,……… …… ……………………8分
,……… …… ……………………8分
则![]() ,
,
![]() ,
,![]() ,
,
所以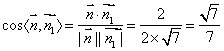 ,… …… …………………………10分
,… …… …………………………10分
由图可知二面角B-FC![]() -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC![]() -C的余弦值为
-C的余弦值为![]() . ……12分
. ……12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014届浙江省高二9月质量检测文科数学试卷(解析版) 题型:解答题
(本题12分)如图,在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB= 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值。

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三全真模拟考试数学文卷 题型:解答题
((本题12分)如图所示,在直四棱柱 中,
中,  ,点
,点 是棱
是棱 上一点
上一点
(1)求证: 面
面 ;
;
(2)求证: ;
;

查看答案和解析>>
科目:高中数学 来源:2011-2012年山东省济宁市高二上学期期中考试文科数学 题型:解答题
(本题12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013届四川省巴中市四县中高二上学期期末考试理科数学 题型:解答题
((本题12分)如图2,在棱长为1的正方体ABCD—A1B1C1D1中,点E、F、G分别是DD1、BD、BB1的中点。
(Ⅰ)求直线EF与直线CG所成角的余弦值;
(Ⅱ)求直线C1C与平面GFC所成角的正弦值;
(Ⅲ)求二面角E—FC—B的余弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com