
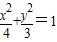 的左右顶点,F为椭圆的右焦点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
的左右顶点,F为椭圆的右焦点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.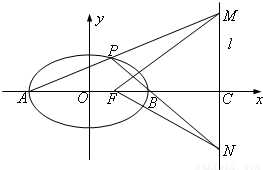
 ),
), .
.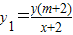 ①
①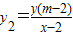 ②
② .
. ,代入上式化简得m2=-8,此式不成立.
,代入上式化简得m2=-8,此式不成立.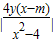
 |,其几何意义是直线CP斜率绝对值的倒数的3倍,
|,其几何意义是直线CP斜率绝对值的倒数的3倍, ,得(3+4k2)x2-8mk2+4k2m2-12=0.
,得(3+4k2)x2-8mk2+4k2m2-12=0.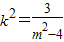 .
. .
. .
.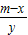 |=
|=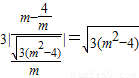 .
. .
.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源:2011届浙江省学军中学高三模拟考试理科数学 题型:解答题
已知A,B是椭圆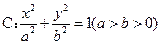 的左,右顶点,
的左,右顶点, ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线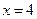 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
(2)求三角形MNT的面积的最大值
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省成都市高三第二次诊断性检测理科数学试卷(解析版) 题型:选择题
已知A、B为椭圆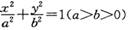 的左、右顶点,C(0,b),直线
的左、右顶点,C(0,b),直线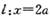 与X轴交于点D,与直线AC交于点P,且BP平分
与X轴交于点D,与直线AC交于点P,且BP平分 ,则此椭圆的离心率为
,则此椭圆的离心率为
(A)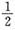 (B)
(B) (C)
(C)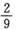 (D)
(D)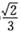
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三模拟考试理科数学 题型:解答题
已知A,B是椭圆 的左,右顶点,
的左,右顶点,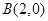 ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
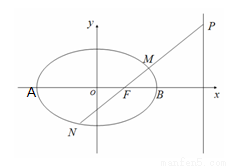
(1)求椭圆C的方程;
(2)求三角形MNT的面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点

(1)求椭圆C的方程;![]()
(2)求三角形MN![]() T的面积的最大值
T的面积的最大值
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市学军中学高三第九次月考数学试卷(理科)(解析版) 题型:解答题
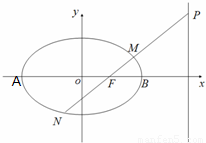 已知A,B是椭圆
已知A,B是椭圆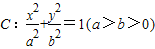 的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
的左,右顶点,B(2,0),过椭圆C的右焦点F的直线交椭圆于点M,N,交直线x=4于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com