
观察下列等式:13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第五个等式为 .
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:解答题
已知函数y=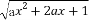 的定义域为R.
的定义域为R.
(1)求a的取值范围.
(2)若函数的最小值为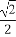 ,解关于x的不等式x2-x-a2-a<0.
,解关于x的不等式x2-x-a2-a<0.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:选择题
若角α,β满足-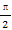 <α<β<π,则α-β的取值范围是( )
<α<β<π,则α-β的取值范围是( )
(A)(-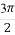 ,
,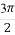 ) (B)(-
) (B)(-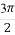 ,0) (C)(0,
,0) (C)(0,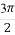 ) (D)(-
) (D)(-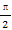 ,0)
,0)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:选择题
设等比数列{an}中,前n项和为Sn,已知S3=8,S6=7,则a7+a8+a9=( )
(A) (B)-
(B)- (C)
(C)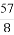 (D)
(D)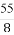
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:解答题
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)
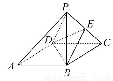
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
记Sn是等差数列{an}前n项的和,Tn是等比数列{bn}前n项的积,设等差数列{an}公差d≠0,若对小于2011的正整数n,都有Sn=S2011-n成立,则推导出a1006=0.设等比数列{bn}的公比q≠1,若对于小于23的正整数n,都有Tn=T23-n成立,则( )
(A)b11=1 (B)b12=1 (C)b13=1 (D)b14=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:解答题
设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an},{bn}的通项公式.
(2)求数列{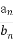 }的前n项和Sn.
}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷(解析版) 题型:选择题
10张奖券中有3张是有奖的,某人从中不放回地依次抽两张,则在第一次抽到中奖券的条件下,第二次也抽到中奖券的概率为( )
(A) (B)
(B) (C)
(C)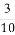 (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com