
【题目】已知曲线![]() 的方程为
的方程为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.当![]() 时,曲线
时,曲线![]() 为椭圆,其焦距为
为椭圆,其焦距为![]()
B.当![]() 时,曲线
时,曲线![]() 为双曲线,其离心率为
为双曲线,其离心率为![]()
C.存在实数![]() 使得曲线
使得曲线![]() 为焦点在
为焦点在![]() 轴上的双曲线
轴上的双曲线
D.当![]() 时,曲线
时,曲线![]() 为双曲线,其渐近线与圆
为双曲线,其渐近线与圆![]() 相切
相切
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】羽毛球比赛中,首局比赛由裁判员采用抛球的方法决定谁先发球,在每回合争夺中,赢方得1分且获得发球权.每一局中,获胜规则如下:①率先得到21分的一方赢得该局比赛;②如果双方得分出现![]() ,需要领先对方2分才算该局获胜;③如果双方得分出现
,需要领先对方2分才算该局获胜;③如果双方得分出现![]() ,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为
,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为![]() ;乙发球时,甲得分的概率为
;乙发球时,甲得分的概率为![]() .
.
(Ⅰ)若![]() ,记“甲以
,记“甲以![]() 赢一局”的概率为
赢一局”的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(Ⅱ)根据对以往甲、乙两名运动员的比赛进行数据分析,得到如下![]() 列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为
列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为![]() ,
,![]() 的值.
的值.
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 100 | |
乙发球 | 60 | 90 | |
总计 | 190 |
①完成![]() 列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
②已知在某局比中,双方战成![]() ,且轮到乙发球,记双方再战
,且轮到乙发球,记双方再战![]() 回合此局比赛结束,求
回合此局比赛结束,求![]() 的分布列与期望.
的分布列与期望.
参考公式: ,其中
,其中![]() .
.
临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边长分别等于a,b,c,列举如下五个条件:①![]() ;②
;②![]() ;③cosA+cos2A=0;④a=4;⑤△ABC的面积等于
;③cosA+cos2A=0;④a=4;⑤△ABC的面积等于![]() .
.
(1)请在五个条件中选择一个(只需选择一个)能够确定角A大小的条件来求角A;
(2)在(1)的结论的基础上,再在所给条件中选择一个(只需选择一个),求△ABC周长的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强学生的冬奥会知识,弘扬奥林匹克精神,北京市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在北京市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:
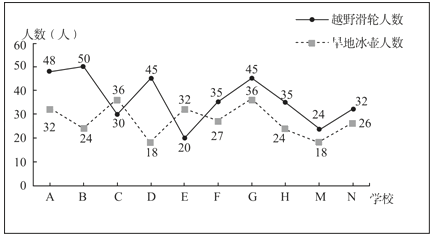
(Ⅰ)现从这10所学校中随机选取2所学校进行调查.求选出的2所学校参与越野滑轮人数都超过40人的概率;
(Ⅱ)现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导,记X为教练选中参加旱地冰壶人数在30人以上的学校个数,求X的分布列和数学期望;
(Ⅲ)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在现代社会中,信号处理是非常关键的技术,我们通过每天都在使用的电话或者互联网就能感受到,而信号处理背后的“功臣”就是正弦型函数.函数 的图象就可以近似的模拟某种信号的波形,则下列说法正确的是( )
的图象就可以近似的模拟某种信号的波形,则下列说法正确的是( )
A.函数![]() 为周期函数,且最小正周期为
为周期函数,且最小正周期为![]()
B.函数![]() 为奇函数
为奇函数
C.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
D.函数![]() 的导函数
的导函数![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是数列1,
是数列1,![]() ,
,![]() ,…,
,…,![]() 的各项和,
的各项和,![]() ,
,![]() .
.
(1)设![]() ,证明:
,证明:![]() 在
在![]() 内有且只有一个零点;
内有且只有一个零点;
(2)当![]() 时,设存在一个与上述数列的首项、项数、末项都相同的等差数列,其各项和为
时,设存在一个与上述数列的首项、项数、末项都相同的等差数列,其各项和为![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)给出由公式![]() 推导出公式
推导出公式![]() 的一种方法如下:在公式
的一种方法如下:在公式![]() 中两边求导得:
中两边求导得:![]() ,所以
,所以![]() 成立,请类比该方法,利用上述数列的末项
成立,请类比该方法,利用上述数列的末项![]() 的二项展开式证明:
的二项展开式证明:![]() 时
时![]() (其中
(其中![]() 表示组合数)
表示组合数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.
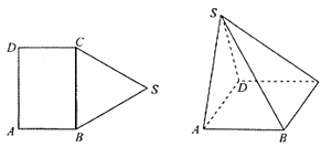
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com