
【题目】羽毛球比赛中,首局比赛由裁判员采用抛球的方法决定谁先发球,在每回合争夺中,赢方得1分且获得发球权.每一局中,获胜规则如下:①率先得到21分的一方赢得该局比赛;②如果双方得分出现![]() ,需要领先对方2分才算该局获胜;③如果双方得分出现
,需要领先对方2分才算该局获胜;③如果双方得分出现![]() ,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为
,先取得30分的一方该局获胜.现甲、乙两名运动员进行对抗赛,在每回合争夺中,若甲发球时,甲得分的概率为![]() ;乙发球时,甲得分的概率为
;乙发球时,甲得分的概率为![]() .
.
(Ⅰ)若![]() ,记“甲以
,记“甲以![]() 赢一局”的概率为
赢一局”的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(Ⅱ)根据对以往甲、乙两名运动员的比赛进行数据分析,得到如下![]() 列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为
列联表部分数据.若不考虑其它因素对比赛的影响,并以表中两人发球时甲得分的频率作为![]() ,
,![]() 的值.
的值.
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 100 | |
乙发球 | 60 | 90 | |
总计 | 190 |
①完成![]() 列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
列联表,并判断是否有95%的把握认为“比赛得分与接、发球有关”?
②已知在某局比中,双方战成![]() ,且轮到乙发球,记双方再战
,且轮到乙发球,记双方再战![]() 回合此局比赛结束,求
回合此局比赛结束,求![]() 的分布列与期望.
的分布列与期望.
参考公式: ,其中
,其中![]() .
.
临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(Ⅰ)![]() (Ⅱ)①列联表见解析,有;②分布列见解析,
(Ⅱ)①列联表见解析,有;②分布列见解析,![]()
【解析】
(Ⅰ)根据题意可得前![]() 个回合里,甲赢下20个回合,输掉
个回合里,甲赢下20个回合,输掉![]() 个回合,且最后一个回合必需获胜,从而得到
个回合,且最后一个回合必需获胜,从而得到![]() ,计算出
,计算出![]() 和
和![]() ,做商比较,得到答案;
,做商比较,得到答案;
(Ⅱ)①根据题意,填写好列联表,计算出![]() ,做出判断;②由列联表得到
,做出判断;②由列联表得到![]() 和
和![]() 的值,得到
的值,得到![]() 可取的值,分别计算其概率,写出分布列,计算出期望.
可取的值,分别计算其概率,写出分布列,计算出期望.
(Ⅰ)∵甲以![]() 获胜,则在这
获胜,则在这![]() 个回合的争夺中,前
个回合的争夺中,前![]() 个回合里,甲赢下20个回合,输掉
个回合里,甲赢下20个回合,输掉![]() 个回合,且最后一个回合必需获胜
个回合,且最后一个回合必需获胜
∴![]() ,
,
∴![]() ,
,![]()
∵ ,
,
∴![]()
(Ⅱ)①由甲发球的总计和乙得分,得到甲得分的数值为![]() ,
,
由乙发球的总计和甲得分,得到乙得分的数值为![]() ,
,
从而得到甲得分总计为![]() ,乙得分的总计为
,乙得分的总计为![]() ,
,
所以![]() 列联表如下:
列联表如下:
甲得分 | 乙得分 | 总计 | |
甲发球 | 50 | 50 | 100 |
乙发球 | 60 | 30 | 90 |
总计 | 110 | 80 | 190 |
![]()
∵![]() ,∴有95%的把握认为“比赛得分与接、发球有关”
,∴有95%的把握认为“比赛得分与接、发球有关”
②由![]() 列联表知
列联表知![]() ,
,![]() ,
,
此局比赛结束,比分可能是![]() ,
,![]() ,
,![]() ,
,
∴![]()
若比分为![]() ,则甲获胜概率为
,则甲获胜概率为![]() ,乙获胜概率为
,乙获胜概率为![]() ,
,
∴![]() ,
,
若比分为![]() ,则甲获胜的情况可能为:甲乙甲甲,乙甲甲甲,
,则甲获胜的情况可能为:甲乙甲甲,乙甲甲甲,
其概率![]() ,
,
乙获胜的情况可能为:甲乙乙乙,乙甲乙乙,
其概率![]() ,
,
∴![]() ,
,
若比分为![]() ,则
,则![]() ,
,
∴![]() 的分布列为
的分布列为
| 2 | 4 | 5 |
|
|
|
|
∴![]()


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为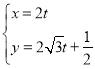 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设动点![]() 在圆
在圆![]() 上,动线段
上,动线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() ,
,![]() 与直线
与直线![]() 交点为
交点为![]() ,且直角坐标系中,
,且直角坐标系中,![]() 点的横坐标大于
点的横坐标大于![]() 点的横坐标,求点
点的横坐标,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数F(x)=min{2|x1|,x22ax+4a2},
,函数F(x)=min{2|x1|,x22ax+4a2},
其中min{p,q}=![]()
(Ⅰ)求使得等式F(x)=x22ax+4a2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如:在十位档拨上一颗上珠和一颗下珠,个位档拨上一颗上珠,则表示数字65.若在个、十、百、千位档中随机选择一档拨一颗上珠,再随机选择两个档位各拨一颗下珠,则所拨数字大于200的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点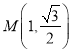 ,
,![]() 的参数方程为
的参数方程为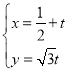 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于
(t为参数),直线l与曲线C分别交于![]() 两点.
两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com