
【题目】为了增强学生的冬奥会知识,弘扬奥林匹克精神,北京市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在北京市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:
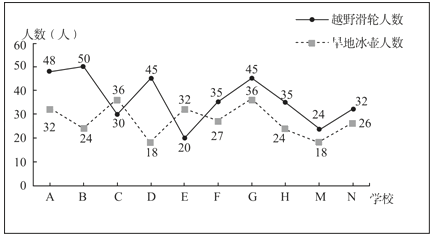
(Ⅰ)现从这10所学校中随机选取2所学校进行调查.求选出的2所学校参与越野滑轮人数都超过40人的概率;
(Ⅱ)现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导,记X为教练选中参加旱地冰壶人数在30人以上的学校个数,求X的分布列和数学期望;
(Ⅲ)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)见解析,
(Ⅱ)见解析,![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)记“选出的两所学校参与越野滑轮人数都超过40人”为事件S,从这10所学校中随机选取2所学校进行调查,可得基本事件总数为![]() .参与越野滑轮人数超过40人的学校共4所,随机选择2所学校共
.参与越野滑轮人数超过40人的学校共4所,随机选择2所学校共![]() 种,利用古典概率计算公式即可得出概率.
种,利用古典概率计算公式即可得出概率.
(Ⅱ)X的所有可能取值为0,1,2,参加旱地冰壶人数在30人以上的学校共4所.利用超几何分布列计算公式即可得出.
(Ⅲ)答案不唯一.示例:虽然概率非常小,但是也可能发生,一旦发生,就有理由认为指导后总考核达到“优”的概率发生了变化.
(Ⅰ)记“选出的两所学校参与越野滑轮人数都超过40人”为事件S,现从这10所学校中随机选取2所学校进行调查,可得基本事件总数为![]() .
.
参与越野滑轮人数超过40人的学校共4所,随机选择2所学校共![]() 种,
种,
所以
(Ⅱ)X的所有可能取值为0,1,2,参加旱地冰壶人数在30人以上的学校共4所.
![]() ,
,![]() ,
,![]() .
.
X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
![]() .
.
(Ⅲ)答案不唯一.
答案示例1:可以认为甲同学在指导后总考核为“优”的概率发生了变化.理由如下:
指导前,甲同学总考核为“优”的概率为:![]() .
.
指导前,甲同学总考核为“优”的概率非常小,一旦发生,就有理由认为指导后总考核达到“优”的概率发生了变化.
答案示例2:无法确定.理由如下:
指导前,甲同学总考核为“优”的概率为:![]() .
.
虽然概率非常小,但是也可能发生,所以,无法确定总考核达到“优”的概率发生了变化.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国诗词大会的播出引发了全民读书热,某学校语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如右图,若规定得分不低于85分的学生得到“诗词达人”的称号,低于85分且不低于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号.根据该次比赛的成绩按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )

A. 6B. 5C. 4D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆,离心率![]() ,且经过抛物线
,且经过抛物线![]() 的焦点.若过点
的焦点.若过点![]() 的直线
的直线![]() 斜率不等于零
斜率不等于零![]() 与椭圆交于不同的两点E、
与椭圆交于不同的两点E、![]() 在B、F之间
在B、F之间![]() ,
,
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 求直线l斜率的取值范围;
求直线l斜率的取值范围;
![]() 若
若![]() 与
与![]() 面积之比为
面积之比为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.当![]() 时,曲线
时,曲线![]() 为椭圆,其焦距为
为椭圆,其焦距为![]()
B.当![]() 时,曲线
时,曲线![]() 为双曲线,其离心率为
为双曲线,其离心率为![]()
C.存在实数![]() 使得曲线
使得曲线![]() 为焦点在
为焦点在![]() 轴上的双曲线
轴上的双曲线
D.当![]() 时,曲线
时,曲线![]() 为双曲线,其渐近线与圆
为双曲线,其渐近线与圆![]() 相切
相切
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() ,
,![]() (1)
(1)![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式,并证明:
的解析式,并证明:![]() .
.
(2)已知![]() ,且函数
,且函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() ,
,![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,
,![]() ,证明:
,证明:![]() (1)
(1)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为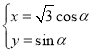 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,点
轴的正半轴为极轴,建立极坐标系,点![]() 的极坐标
的极坐标![]() ,直线
,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的标准参数方程;
的标准参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com