
【题目】已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() ,线段
,线段![]() 的中垂线
的中垂线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)是否存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,若存在,请求出
四点共圆,若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
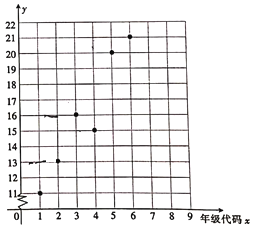
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数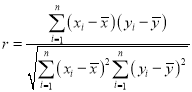 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=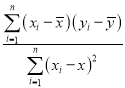 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为底面
为底面![]() 的重心.
的重心.
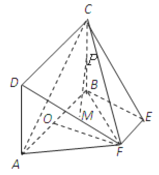
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂过去在生产过程中将污水直接排放到河流中对沿河环境造成了一定的污染,根据环保部门对该厂过去10年的监测数据,统计出了其每年污水排放量![]() (单位:吨)的频率分布表:
(单位:吨)的频率分布表:
污水排放量 |
|
|
|
|
频率 | 0.1 | 0.3 | 0.4 | 0.2 |
将污水排放量落入各组的频率作为概率,并假设每年该厂污水排放量相互独立.
(1)若不加以治理,根据上表中的数据,计算未来3年中至少有2年污水排放量不小于200吨的概率;
(2)根据环保部门的评估,该厂当年污水排放量![]() 时,对沿河环境及经济造成的损失为5万元;当年污水排放量
时,对沿河环境及经济造成的损失为5万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为10万元;当年污水排放量
时,对沿河环境及经济造成的损失为10万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为20万元;当年污水排放量
时,对沿河环境及经济造成的损失为20万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
方案1:若该厂不采取治污措施,则需全部赔偿对沿河环境及经济造成的损失;
方案2:若该厂采购治污设备对所有产生的污水净化达标后再排放,则不需赔偿,采购设备的费用为10万元,每年设备维护等费用为15万元,该设备使用10年需重新更换.在接下来的10年里,试比较上述2种方案哪种能为该厂节约资金,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,2Sn+2n=an+1﹣2,a2=8,其中n∈N*.
(1)记bn=an+1,求证:{bn}是等比数列;
(2)设![]() 为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com