
【题目】如图,在三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 上的投影
上的投影![]() 在棱
在棱![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
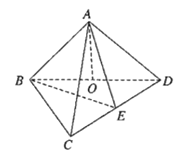
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)已知点![]() 为
为![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)见解析(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)由题知:![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .又根据勾股定理得到
.又根据勾股定理得到![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)首先以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,轴的正方向,建立空间直角坐标系,找到相应点的坐标,再分别求出平面
轴,轴的正方向,建立空间直角坐标系,找到相应点的坐标,再分别求出平面![]() 和平面
和平面![]() 的法向量,带入公式计算即可.
的法向量,带入公式计算即可.
(3)首先设![]() ,
,![]() ,根据
,根据![]() 平面
平面![]() ,得到
,得到![]() ,即可求出
,即可求出![]() ,再计算
,再计算![]() 即可.
即可.
(1)因为顶点![]() 在底面
在底面![]() 上的射影
上的射影![]() 在棱
在棱![]() 上,
上,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
由![]() ,
,![]() ,
,
得![]() ,所以
,所以![]() ,
,
因为![]() 且
且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
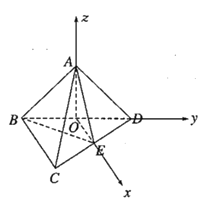
(2)连接![]() ,
,
因为![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,
所以![]() ,
,
如图,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,轴的正方向,建立空间直角坐标系,
轴,轴的正方向,建立空间直角坐标系,
![]() ,
,
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则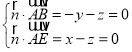 .取
.取![]() ,得
,得![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则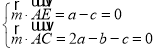 ,取
,取![]() ,则
,则![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)设![]() ,
,![]() ,
,![]()
因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右顶点分别为
的左右顶点分别为![]() ,
,![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 、
、![]() 的任意一点,设直线
的任意一点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,且
,且![]() ,椭圆的焦距长为4.
,椭圆的焦距长为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,分别记
两点,分别记![]() ,
,![]() 的面积为
的面积为![]() 、
、![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中记载了这样的一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”,其大意为:有一个人走了378里路,第一天健步行走,从第二天起其因脚痛每天走的路程为前一天的一半,走了6天后到达了目的地,问此人第三天走的路程里数为( )
A.192B.48C.24D.88
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是曲线
是曲线![]() 截直线
截直线![]() 所得线段的中点,求
所得线段的中点,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共11只,现在盒子上开一小孔,每次只能飞出1只昆虫(假设任意1只昆虫等可能地飞出).若有2只昆虫先后任意飞出(不考虑顺序),则飞出的是蝴蝶或蜻蜓的概率是![]() .
.
(1)求盒子中蜜蜂有几只;
(2)若从盒子中先后任意飞出3只昆虫(不考虑顺序),记飞出蜜蜂的只数为X,求随机变量X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+1,g(x)=4x+1,的定义域都是集合A,函数f(x)和g(x)的值域分别为S和T,
(1)若A=[1,2],求S∩T
(2)若A=[0,m]且S=T,求实数m的值
(3)若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com