
分析 根据购买的总费用=茶壶的费用+茶杯的费用,建立关系式就可以了;分3种情况讨论,当y1>y2,y1=y2,y1<y2时分别求出x的值即可.
解答 解:优惠办法(1):y1=4×20+(x-4)×5=5x+60(x≥4,x∈N*),
优惠办法(2):y2=0.92(4×20+5x)=4.6x+73.6(x≥4,x∈N*)
当y1=y2,5x+60=4.6x+73.6,解得:x=34
∵x≥4,x∈N*,
∴当4≤x<34时,优惠办法(1)省钱;当x=34时,两种方法一样优惠;当x>34时,优惠办法(2)省钱.
点评 本题考查了单价×数量=总价的运用,一次函数的解析式的运用,方案设计的运用,解答时求出函数的解析式是关键.


科目:高中数学 来源: 题型:解答题
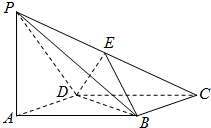 如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点.
如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.
如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD-A1B1C1D1中,点E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com