
����Ŀ��������ij��ϴ�Ӽ��²�Ʒʱ����ͬ���Ӽ��������Լ����ӵ�˳��Բ�Ʒ�����ʶ���Ӱ�죬��Ҫ�Ը��ֲ�ͬ�Ĵ��䷽ʽ��ʵ����бȽ�.���з���ȷֱ�Ϊ1��2��3��4��5��6���������Ӽ��ɹ�ѡ�ã������������ԭ������Ҫ���ѡȡ���ֲ�ͬ�����Ӽ��Ⱥ����ӽ���ʵ��.
(1)���������Ӽ������֮�͵���5�ĸ��ʣ�
(2)���������Ӽ������֮�ʹ���5���Һ����ӵ����Ӽ�����Ƚϴ�ĸ���.
���𰸡���1��![]() ����2��
����2��![]()
����������������1�������оٷ������е�ѡ������![]() ���������㡰�������Ӽ������֮�͵���5����ѡ�����оٷ����ֻ��4�����ɴ�������ֲ�ͬ�����Ӽ��ķ����֮�͵���5�ĸ�������2�����оٷ���á��������Ӽ������֮�ʹ���5���Һ����ӵ����Ӽ�����Ƚϴ������й�11�֣���ϣ�1�����ùŵ�����ʹ�ʽ�ɵý��.
���������㡰�������Ӽ������֮�͵���5����ѡ�����оٷ����ֻ��4�����ɴ�������ֲ�ͬ�����Ӽ��ķ����֮�͵���5�ĸ�������2�����оٷ���á��������Ӽ������֮�ʹ���5���Һ����ӵ����Ӽ�����Ƚϴ������й�11�֣���ϣ�1�����ùŵ�����ʹ�ʽ�ɵý��.
������������������ӵ����Ӽ������Ϊ![]() �������ӵ�Ϊ
�������ӵ�Ϊ![]() ����������Ϊ
����������Ϊ![]() ��������¼�������
��������¼�������
![]()
![]() ,��30�ֽ��.
,��30�ֽ��.
(1)�衰�������Ӽ������֮�͵���5��Ϊ�¼�![]() ��
��
���¼�![]() �����Ľ����
�����Ľ����![]() ����4�֣���
����4�֣���![]() .
.
(2)�衰�������Ӽ������֮�ʹ���5���Һ����ӵ����Ӽ�����Ƚϴ�Ϊ�¼�![]() ��
��
���¼�![]() �����Ľ����
�����Ľ����![]() ����11�֣���
����11�֣���![]() .
.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƻ���ijˮ�⽨һ�����లװ ![]() ̨�������ˮ��վ����ȥ
̨�������ˮ��վ����ȥ ![]() ���ˮ��������ʾ��ˮ����������
���ˮ��������ʾ��ˮ���������� ![]() ������������һ����������ˮ�������ˮ֮�ͣ���λ���������ף�����40���ϣ�����
������������һ����������ˮ�������ˮ֮�ͣ���λ���������ף�����40���ϣ����� ![]() �������
������� ![]() �꣬������
�꣬������ ![]() �Ҳ�����
�Ҳ����� ![]() �������
������� ![]() �꣬����
�꣬���� ![]() �������
������� ![]() �꣬�������������������ε�Ƶ����Ϊ��Ӧ�εĸ��ʣ������������������������
�꣬�������������������ε�Ƶ����Ϊ��Ӧ�εĸ��ʣ������������������������
��1����δ�� ![]() ���У���
���У��� ![]() ��ʾ��������
��ʾ�������� ![]() ����������
���������� ![]() �ķֲ��м�������
�ķֲ��м�������
��2��ˮ��վϣ����װ�ķ�������������У���ÿ�귢�����������̨������������ ![]() ���ƣ��������¹�ϵ��
���ƣ��������¹�ϵ��
�������� |
|
|
|
�������������̨�� | 1 |
|
|
��ij̨��������У����̨������Ϊ ![]() ��Ԫ����ij̨�����δ���У����̨�����
��Ԫ����ij̨�����δ���У����̨����� ![]() ��Ԫ����ʹˮ��վ��������ľ�ֵ�ﵽ���Ӧ��װ���������̨��
��Ԫ����ʹˮ��վ��������ľ�ֵ�ﵽ���Ӧ��װ���������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c��c��a=2acosB���� ![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����漸�����������������������ǣ� ��
A.ijУ����(1)����55�ˣ�2����54�ˣ�3����52�ˣ��ɴ˵ø������а���������50��
B.����ֱ��ƽ�У�ͬ���ڽǻ����������A���B������ƽ��ֱ�ߵ�ͬ���ڽǣ����A����B��180��
C.��ƽ�������ε����ʣ��Ʋ�ռ��ı��ε�����
D.������{an}��a1��1��an�� ![]() (an��1��
(an��1�� ![]() )(n��2)���ɴ˹��ɳ�{an}��ͨ�
)(n��2)���ɴ˹��ɳ�{an}��ͨ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����Բ ![]() =1��a��b��0�������ҽ���ֱ�ΪF1 �� F2 �� �Ҷ���ΪA���϶���ΪB��������Ϊe����Բ��һ��C���㣺C��x���Ϸ�����CF1��x�ᣮ
=1��a��b��0�������ҽ���ֱ�ΪF1 �� F2 �� �Ҷ���ΪA���϶���ΪB��������Ϊe����Բ��һ��C���㣺C��x���Ϸ�����CF1��x�ᣮ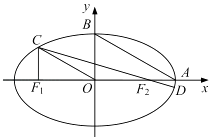
��1����OC��AB����e��ֵ��
��2������CF2���ӳ�����Բ����һ��D�� ![]() ��e��
��e�� ![]() ����
���� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xe2x��lnx��ax��
��1����a=0ʱ������f��x����[ ![]() ��1]�ϵ���Сֵ��
��1]�ϵ���Сֵ��
��2����x��0������ʽf��x����1���������a��ȡֵ��Χ��
��3����x��0������ʽf�� ![]() ����1��
����1�� ![]() e
e ![]() +
+ ![]() ���������a��ȡֵ��Χ��
���������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ƽԭ�����������ķ����֮һ�������������������ڼ��㣬���Ǵ����������ļ���ϵͳ�����п�ƽ���㷨������д����Եģ������ͼ��ͼ��ʾ��������a��n���ε�ֵ�ֱ�Ϊ8��2��0.5����ÿ�����㶼��ȷ��С�������λ����������Ϊ�� �� 
A.2.81
B.2.82
C.2.83
D.2.84
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λѧ���μ���ѧ������ѵ������ѵ�ڼ����Dzμӵ�5��Ԥ���ɼ���¼���£�
�ף�82��82��79��95��87
�ң�95��75��80��90��85
��1���þ�Ҷͼ��ʾ���������ݣ�
��2����ס������˳ɼ���ƽ�����뷽�
��3������Ҫ����ѡ��һ�˲μ���ѧ����������Ϊѡ����λѧ���μӺ��ʣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ������ϵ ![]() �У�����
�У����� ![]() �IJ�������Ϊ
�IJ�������Ϊ ![]() ������
������ ![]() ������������
������������ ![]() ��
�� ![]() ��������ԭ��
��������ԭ�� ![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ.
���������Ϊ���Ὠ��������ϵ.
��1�������� ![]() ����ͨ���̺�����
����ͨ���̺����� ![]() �ļ����귽�̣�
�ļ����귽�̣�
��2�������� ![]() ��
�� ![]() ��������
�������� ![]() ��
�� ![]() �ֱ���
�ֱ��� ![]() ��
�� ![]() ���㣬��
���㣬�� ![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com