
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.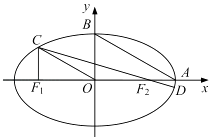
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)
解:椭圆 ![]() =1(a>b>0)的焦距为2c,
=1(a>b>0)的焦距为2c,
由CF1⊥x轴.则C(﹣c,y0),y0>0,
由C在椭圆上,则y0= ![]() ,则C(﹣c,
,则C(﹣c, ![]() ),
),
由OC∥AB,则﹣ ![]() =kOC=kAB=﹣
=kOC=kAB=﹣ ![]() ,则b=c,
,则b=c,
e= ![]() =
= ![]() =
= ![]() ,
,
e的值 ![]()
(2)
解:设D(x1,y1),设 ![]() =λ
=λ ![]() ,
,
C(﹣c, ![]() ),F2(c,0),
),F2(c,0),
故 ![]() =(2c,﹣
=(2c,﹣ ![]() ),
), ![]() =(x1﹣c,y1),
=(x1﹣c,y1),
由 ![]() =λ
=λ ![]() ,则2c=λ(x1﹣c),﹣
,则2c=λ(x1﹣c),﹣ ![]() =λy1,则D(
=λy1,则D( ![]() c,﹣
c,﹣ ![]() ),
),
由点D在椭圆上,则( ![]() )2e2+
)2e2+ ![]() =1,整理得:(λ2+4λ+3)e2=λ2﹣1,
=1,整理得:(λ2+4λ+3)e2=λ2﹣1,
由λ>0,e2= ![]() =
= ![]() =1﹣
=1﹣ ![]() ,
,
由 ![]() ≤e≤
≤e≤ ![]() ,则
,则 ![]() ≤e2≤
≤e2≤ ![]() ,则
,则 ![]() ≤1﹣
≤1﹣ ![]() ≤
≤ ![]() ,
,
解得: ![]() ≤λ≤5,
≤λ≤5,
∴ ![]() 的取值范围[
的取值范围[ ![]() ,5]
,5]
【解析】(1)由CF1⊥x轴.则C(﹣c, ![]() ),根据直线的斜率相等,即可求得b=c,利用离心率公式即可求得e的值;(2)根据向量的坐标运算,求得D点坐标,代入椭圆方程,求得e2=
),根据直线的斜率相等,即可求得b=c,利用离心率公式即可求得e的值;(2)根据向量的坐标运算,求得D点坐标,代入椭圆方程,求得e2= ![]() =1﹣
=1﹣ ![]() ,由离心率的取值范围,即可求得λ的取值范围.
,由离心率的取值范围,即可求得λ的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 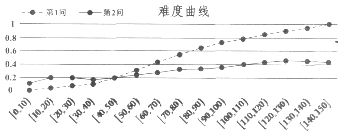
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
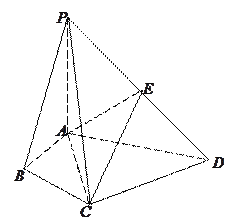
【题目】在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,![]() =2
=2![]() =2.
=2.
(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在试制某种洗涤剂新产品时,不同添加剂的种类以及添加的顺序对产品的性质都有影响,需要对各种不同的搭配方式做实验进行比较.现有芳香度分别为1,2,3,4,5,6的六种添加剂可供选用,根据试验设计原理,需要随机选取两种不同的添加剂先后添加进行实验.
(1)求两种添加剂芳香度之和等于5的概率;
(2)求两种添加剂芳香度之和大于5,且后添加的添加剂芳香度较大的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(1)求数列{an}和{bn}的通项公式;
(2)令cn=anbn , 设数列{cn}的前n项和为Tn , 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com