
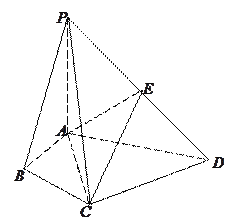
【题目】在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,![]() =2
=2![]() =2.
=2.
(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
【答案】(1)见解析(2)见解析
【解析】分析:(1)取PC中点F,利用等腰三角形的性质可得PC⊥AF,先证明CD⊥平面PAC,可得CD⊥PC,从而EF⊥PC,故有PC⊥平面AEF,进而证得PC⊥AE.
(2)取AD中点M,利用三角形的中位线证明EM∥平面PAB,利用同位角相等证明MC∥AB,得到平面EMC∥平面PAB,证得EC∥平面PAB.
详解:(1)在Rt△ABC中,AB=1,∠BAC=60°,
∴BC=![]() ,AC=2.取
,AC=2.取![]() 中点
中点![]() ,连AF, EF,
,连AF, EF,
∵PA=AC=2,∴PC⊥![]() .
.
∵PA⊥平面ABCD,![]() 平面ABCD,
平面ABCD,
∴PA⊥![]() ,又∠ACD=90°,即
,又∠ACD=90°,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴PC⊥![]() .
.
(2)证法一:取AD中点M,连EM,CM.则
EM∥PA.∵EM ![]() 平面PAB,PA
平面PAB,PA![]() 平面PAB,
平面PAB,
∴EM∥平面PAB.
在Rt△ACD中,∠CAD=60°,AC=AM=2,
∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.
∵MC ![]() 平面PAB,AB
平面PAB,AB![]() 平面PAB,
平面PAB,
∴MC∥平面PAB.
∵EM∩MC=M,∴平面EMC∥平面PAB.
∵EC![]() 平面EMC,∴EC∥平面PAB.
平面EMC,∴EC∥平面PAB.
证法二:延长DC、AB,设它们交于点N,连PN.
∵∠NAC=∠DAC=60°,AC⊥CD,∴C为ND的中点
∵E为PD中点,∴EC∥PN
∵EC ![]() 平面PAB,PN
平面PAB,PN![]() 平面PAB,∴EC∥平面PAB.
平面PAB,∴EC∥平面PAB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】现有4个人参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求出4个人中恰有2个人去 参加甲游戏的概率;
(2)求这4个人中去参加甲游戏人数大于去参加乙游戏的人数的概率;
(3)用 ![]() 分别表示这4个人中去参加甲、乙游戏的人数,记
分别表示这4个人中去参加甲、乙游戏的人数,记 ![]() ,求随机变量
,求随机变量 ![]() 的分布列与数学期望
的分布列与数学期望 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 仍为数列
仍为数列![]() 中的项,若存在,求出所有满足的正整数
中的项,若存在,求出所有满足的正整数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,
, ![]() ,点
,点 ![]() 在椭圆上,
在椭圆上, ![]() ,且
,且 ![]() 的面积为4.
的面积为4.
(1)求椭圆的方程;
(2)点 ![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 分别是椭圆的左、右顶点,直线
分别是椭圆的左、右顶点,直线 ![]() 与直线
与直线 ![]() 分别交于
分别交于 ![]() 两点,试证:以
两点,试证:以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于定点,并求该定点的坐标.
轴于定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t ≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数,t ≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2: ![]() ,C3:
,C3: ![]() .
.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.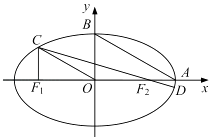
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为1的球O内切于正四面体A﹣BCD,线段MN是球O的一条动直径(M,N是直径的两端点),点P是正四面体A﹣BCD的表面上的一个动点,则 ![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a、b、c是空间中互不重合的三条直线,下面给出五个命题:
①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;
③若a与b相交,b与c相交,则a与c相交;
④若a![]() 平面α,b
平面α,b![]() 平面β,则a,b一定是异面直线;
平面β,则a,b一定是异面直线;
⑤若a,b与c成等角,则a∥b.
上述命题中正确的是________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com