
【题目】已知函数 ![]() (
( ![]() )
)
(1)求函数 ![]() 的单调增区间;
的单调增区间;
(2)若函数 ![]() 在
在 ![]() 上的最小值为
上的最小值为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:由题意, ![]() 的定义域为
的定义域为 ![]() ,且
,且 ![]() .
.
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 的单调增区间为
的单调增区间为 ![]() .
.
当 ![]() 时,令
时,令 ![]() ,得
,得 ![]() ,∴
,∴ ![]() 的单调增区间为
的单调增区间为 ![]() .
.
(2)解:由(1)可知, ![]() .
.
若 ![]() ,则
,则 ![]() ,即
,即 ![]() 在
在 ![]() 上恒成立,
上恒成立, ![]() 在
在 ![]() 上为增函数,
上为增函数,
∴ ![]() ,∴
,∴ ![]() (舍去).
(舍去).
若 ![]() ,则
,则 ![]() ,即
,即 ![]() 在
在 ![]() 上恒成立,
上恒成立, ![]() 在
在 ![]() 上为减函数,
上为减函数,
∴ ![]() ,∴
,∴ ![]() (舍去).
(舍去).
若 ![]() ,当
,当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 在
在 ![]() 上为减函数,
上为减函数,
当 ![]() 时,
时, ![]() ,所以
,所以 ![]() 上为增函数,
上为增函数,
∴ ![]() ,∴
,∴ ![]()
综上所述, ![]() .
.
【解析】(1)先求函数f(x)的定义域,再求f![]() (x),对参数a进行分类讨论,由f
(x),对参数a进行分类讨论,由f![]() (x)
(x)![]() 0得到函数f(x)的单调增区间;(2)由(1)可知f
0得到函数f(x)的单调增区间;(2)由(1)可知f![]() (x),对参数a进行分类讨论,由f
(x),对参数a进行分类讨论,由f![]() (x)
(x)![]() 0(f
0(f![]() (x)
(x)![]() 0)得到函数f(x)的单调增(减)区间,确定函数f(x)的最小值,从而得到参数a的值.
0)得到函数f(x)的单调增(减)区间,确定函数f(x)的最小值,从而得到参数a的值.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.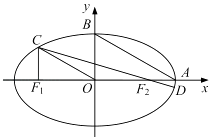
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.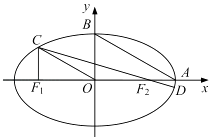
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( ) 
A.2.81
B.2.82
C.2.83
D.2.84
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为1的球O内切于正四面体A﹣BCD,线段MN是球O的一条动直径(M,N是直径的两端点),点P是正四面体A﹣BCD的表面上的一个动点,则 ![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=an+2n+1,数列{bn}的前n项和为Tn..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线
轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,直线
,直线 ![]() 的参数方程为
的参数方程为![]() (
( ![]() 为参数,
为参数, ![]() 为直线的倾斜角).
为直线的倾斜角).
(1)写出直线 ![]() 的普通方程和曲线
的普通方程和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 与曲线
与曲线 ![]() 有唯一的公共点,求角
有唯一的公共点,求角 ![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com