
【题目】计划在某水库建一座至多安装 ![]() 台发电机的水电站,过去
台发电机的水电站,过去 ![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量 ![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足 ![]() 的年份有
的年份有 ![]() 年,不低于
年,不低于 ![]() 且不超过
且不超过 ![]() 的年份有
的年份有 ![]() 年,超过
年,超过 ![]() 的年份有
的年份有 ![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来 ![]() 年中,设
年中,设 ![]() 表示流量超过
表示流量超过 ![]() 的年数,求
的年数,求 ![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量 ![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 |
|
|
若某台发电机运行,则该台年利润为 ![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损 ![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【答案】
(1)解:依题意, ![]() ,
,
由二项分布可知, ![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以 ![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
P | 0.729 | 0.243 | 0.027 | 0.001 |
![]()
(2)解:记水电站的总利润为 ![]() (单位:万元),
(单位:万元),
①假如安装1台发点机,由于水库年入流总量大于40,故一台发电机运行的概率为1,对应的年
利润 ![]() ,
, ![]() ;
;
②若安装2台发电机,
当 ![]() 时,只一台发电机运行,此时
时,只一台发电机运行,此时 ![]() ,
, ![]() ,
,
当 ![]() 时,2台发电机运行,此时
时,2台发电机运行,此时 ![]() ,
, ![]() ,
,
![]() .
.
③若安装3台发电机,
当 ![]() 时,1台发电机运行,此时
时,1台发电机运行,此时 ![]() ,
, ![]() ,
,
当 ![]() 时,2台发电机运行,此时
时,2台发电机运行,此时 ![]() ,
, ![]() ,
,
当 ![]() 时,3台发电机运行,此时
时,3台发电机运行,此时 ![]() ,
, ![]() ,
,
![]()
综上可知,欲使总利润的均值达到最大,应安装2台发电机
【解析】(1)根据题意 P ( X > 120 ) = 0.1 ,由二项分布 ξ ~ B ( 3 , 0.1 )计算出对应的概率值,写出 ξ 的分布列,计算出数学的期望值即可。(2)根据题意结合已知条件分情况讨论得出年利润E(Y)的值,比较即可得出结论。


科目:高中数学 来源: 题型:
【题目】根据平面向量基本定理,若![]() 为一组基底,同一平面的向量
为一组基底,同一平面的向量![]() 可以被唯一确定地表示为
可以被唯一确定地表示为 ![]() =
= ![]() ,则向量
,则向量![]() 与有序实数对
与有序实数对![]() 一一对应,称
一一对应,称![]() 为向量
为向量![]() 的基底
的基底![]() 下的坐标;特别地,若
下的坐标;特别地,若![]() 分别为
分别为![]() 轴正方向的单位向量
轴正方向的单位向量![]() ,则称
,则称![]() 为向量
为向量![]() 的直角坐标.
的直角坐标.
(I)据此证明向量加法的直角坐标公式:若![]() ,则
,则![]() ;
;
(II)如图,直角![]() 中,
中, ![]() ,
, ![]() 点在
点在![]() 上,且
上,且![]() ,求向量
,求向量![]() 在基底
在基底![]() 下的坐标.
下的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 数列
数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求
时,求![]() ;
;
(2)当![]() 时,
时,
(ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(ⅱ)若对任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,
,
求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线  (
( ![]() 为参数)以坐标原点为极点,
为参数)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)将曲线 ![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设点M的直角坐标为 ![]() ,直线l与曲线C的交点为A,B,求
,直线l与曲线C的交点为A,B,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数 ![]() 的图象上每个点的横坐标扩大到原来的4倍,再向左平移
的图象上每个点的横坐标扩大到原来的4倍,再向左平移 ![]() ,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
,得到函数g(x)的图象,则函数g(x)的一个单调递减区间为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 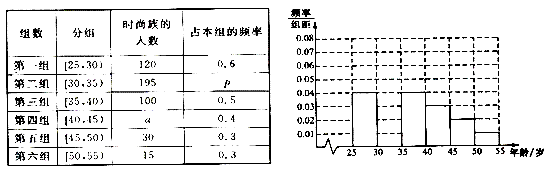
完成以下问题:
(Ⅰ)补全频率分布直方图并求n , a , p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在试制某种洗涤剂新产品时,不同添加剂的种类以及添加的顺序对产品的性质都有影响,需要对各种不同的搭配方式做实验进行比较.现有芳香度分别为1,2,3,4,5,6的六种添加剂可供选用,根据试验设计原理,需要随机选取两种不同的添加剂先后添加进行实验.
(1)求两种添加剂芳香度之和等于5的概率;
(2)求两种添加剂芳香度之和大于5,且后添加的添加剂芳香度较大的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com