
【题目】如图为一块边长为2km的等边三角形地块ABC,为响应国家号召,现对这块地进行绿化改造,计划从BC的中点D出发引出两条成60°角的线段DE和DF,与AB和AC围成四边形区域AEDF,在该区域内种上草坪,其余区域修建成停车场,设∠BDE=![]() .
.
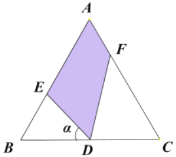
(1)当![]() =60°时,求绿化面积;
=60°时,求绿化面积;
(2)试求地块的绿化面积![]() 的取值范围.
的取值范围.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点是
的焦点是![]() ,直线
,直线![]() :
:![]() ,
,![]() :
:![]() 分别与抛物线
分别与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() ,过
,过![]() ,
,![]() 的直线与圆
的直线与圆![]() :
:![]() 相切.
相切.

(1)求直线![]() 的方程(含
的方程(含![]() 、
、![]() );
);
(2)若线段![]() 与圆
与圆![]() 交于点
交于点![]() ,线段
,线段![]() 与圆
与圆![]() 交于点
交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,圆
,圆![]() 经过点
经过点![]() .
.
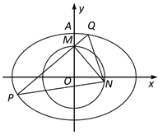
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() 于另一点
于另一点![]() .若△PQN的面积为3,求直线
.若△PQN的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的数据作了初步处理,得到下面的散点图及一些统计量的值.
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中![]()
(I)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为蔬菜农药残量
,哪一个适宜作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)若用解析式![]()
![]() 与用水量
与用水量![]() 的回归方程,求出
的回归方程,求出![]() 与
与![]() 的回归方程.(c,d精确到0.1)
的回归方程.(c,d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )
)
附:参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率( | 级数 | 全月应纳税所得额 | 税率( |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 (元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若直线l:x+y=0与圆C交于A,B两点,求弦AB的长;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一年之计在于春,一日之计在于晨,春天是播种的季节,是希望的开端.某种植户对一块地的![]() 个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为
个坑进行播种,每个坑播3粒种子,每粒种子发芽的概率均为![]() ,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
,且每粒种子是否发芽相互独立.对每一个坑而言,如果至少有两粒种子发芽,则不需要进行补播种,否则要补播种.
(1)当![]() 取何值时,有3个坑要补播种的概率最大?最大概率为多少?
取何值时,有3个坑要补播种的概率最大?最大概率为多少?
(2)当![]() 时,用
时,用![]() 表示要补播种的坑的个数,求
表示要补播种的坑的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
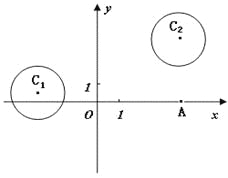
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com