
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若直线![]() 是函数
是函数![]() 的切线,求实数
的切线,求实数![]() 的值;
的值;
(3)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() 在区间
在区间![]() 上单调递增.(2)
上单调递增.(2)![]() (3)见证明
(3)见证明
【解析】
(1)先由解析式,得到函数定义域,对函数求导,根据![]() ,即可得出结果;
,即可得出结果;
(2)先设切点为![]() ,根据切线方程为
,根据切线方程为![]() ,得到
,得到![]() ,再对函数求导,得到
,再对函数求导,得到![]() ,设
,设![]() ,用导数方法研究其单调性,得到最值,即可求出结果;
,用导数方法研究其单调性,得到最值,即可求出结果;
(3)先对函数求导,设![]() ,用导数方法研究
,用导数方法研究![]() 单调性,进而可判断出
单调性,进而可判断出![]() 单调性,即可得出结论成立.
单调性,即可得出结论成立.
解:(1)函数![]() 的定义域为
的定义域为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增.
上单调递增.
(2)设切点为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,得
,得![]() ,
,
所以![]() .
.
设![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() .
.
因为方程![]() 仅有一解
仅有一解![]() ,
,
所以![]() .
.
(3)因为![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增.
单调递增.
因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]()
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一块边长为2km的等边三角形地块ABC,为响应国家号召,现对这块地进行绿化改造,计划从BC的中点D出发引出两条成60°角的线段DE和DF,与AB和AC围成四边形区域AEDF,在该区域内种上草坪,其余区域修建成停车场,设∠BDE=![]() .
.
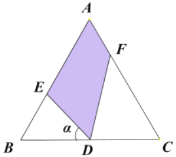
(1)当![]() =60°时,求绿化面积;
=60°时,求绿化面积;
(2)试求地块的绿化面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
,![]() ,
,![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,且
,且![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,且
,且![]() ,得空间几何体
,得空间几何体![]() (图2).直线
(图2).直线![]() 与平面
与平面![]() 所成角的正切值是
所成角的正切值是![]() .
.
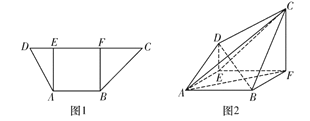
(1)求证:![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为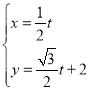 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求直线![]() 被曲线
被曲线![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研发了两种具有自主知识产权的操作系统,分别命名为“天下”、“东方”.这两套操作系统均适用于手机、电脑、车联网、物联网等,且较国际同类操作系统更加流畅.
(1)为了解喜欢“天下”系统是否与性别有关,随机调查了![]() 名男用户和
名男用户和![]() 名女用户,每位用户对“天下”系统给出喜欢或不喜欢的评价,得到下面列联表:
名女用户,每位用户对“天下”系统给出喜欢或不喜欢的评价,得到下面列联表:

请问:能否有![]() 的把握认为男、女用户对“天下”系统的喜欢有差异?
的把握认为男、女用户对“天下”系统的喜欢有差异?
附: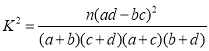 .
.

(2)该公司选定![]() 万名用户对“天下”和“东方”操作系统(以下简称“天下”、“东方”)进行测试,每个用户只能从“天下”或“东方”中选择一个使用,每经过一个月后就给用户一次重新选择“天下”或“东方”的机会.这个月选择“天下”的用户在下个月选择“天下”的概率均为
万名用户对“天下”和“东方”操作系统(以下简称“天下”、“东方”)进行测试,每个用户只能从“天下”或“东方”中选择一个使用,每经过一个月后就给用户一次重新选择“天下”或“东方”的机会.这个月选择“天下”的用户在下个月选择“天下”的概率均为![]() ,选择“东方”的概率均为
,选择“东方”的概率均为![]() ,
,![]() ;这个月选择“东方”的用户在下个月选择“天下”的概率均为
;这个月选择“东方”的用户在下个月选择“天下”的概率均为![]() ,选择“东方”的概率均为
,选择“东方”的概率均为![]() ,
,![]() .记
.记![]() 表示第
表示第![]() 个月用户选择“天下”的概率,已知
个月用户选择“天下”的概率,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(ⅰ)求![]() 的值;
的值;
(ⅱ)证明:数列![]() (
(![]() )为等比数列;
)为等比数列;
(ⅲ)预测选择“天下”操作系统的用户数量不超过多少万人.(精确到1万)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: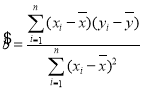 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com