
【题目】椭圆![]() 的一条弦被点
的一条弦被点![]() 平分,则此弦所在的直线方程是( )
平分,则此弦所在的直线方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
设过A点的直线与椭圆两交点的坐标,分别代入椭圆方程,得到两个关系式,分别记作①和②,①﹣②后化简得到一个关系式,然后根据A为弦EF的中点,由A的坐标求出E和F两点的横纵坐标之和,表示出直线EF方程的斜率,把化简得到的关系式变形,将E和F两点的横纵坐标之和代入即可求出斜率的值,然后由点A的坐标和求出的斜率写出直线EF的方程即可.
设过点A的直线与椭圆相交于两点,E(x1,y1),F(x2,y2),
则有![]() ①,
①,![]() ②,
②,
①﹣②式可得:![]()
又点A为弦EF的中点,且A(4,2),∴x1+x2=8,y1+y2=4,
∴![]() (x1﹣x2)﹣
(x1﹣x2)﹣![]() (y1﹣y2)=0
(y1﹣y2)=0
即得kEF=![]()
∴过点A且被该点平分的弦所在直线的方程是y﹣2=﹣![]() (x﹣4),即x+2y﹣8=0.
(x﹣4),即x+2y﹣8=0.
故选:D.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在40分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上为优分(含80分),请你根据已知条件作出2×2列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题![]() ,
,![]() 都是假命题,则命题“
都是假命题,则命题“![]() ”为真命题.
”为真命题.
B. ![]() ,函数
,函数![]() 都不是奇函数.
都不是奇函数.
C. 函数![]() 的图像关于
的图像关于![]() 对称 .
对称 .
D. 将函数![]() 的图像上所有点的横坐标伸长到原来的2倍后得到
的图像上所有点的横坐标伸长到原来的2倍后得到![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() ,其中
,其中![]() ,
,![]() 为实数,事件
为实数,事件![]() 为“函数
为“函数![]() 在区间
在区间![]() 为增函数”.
为增函数”.
(1)若![]() 为区间
为区间![]() 上的整数值随机数,
上的整数值随机数,![]() 为区间
为区间![]() 上的整数值随机数,求事件
上的整数值随机数,求事件![]() 发生的概率;
发生的概率;
(2)若![]() 为区间
为区间![]() 上的均匀随机数,
上的均匀随机数,![]() 为区间
为区间![]() 上的均匀随机数,求事件
上的均匀随机数,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() .
.
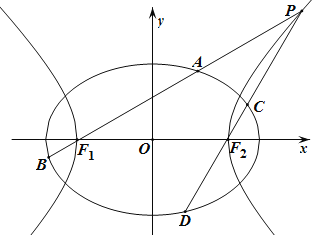
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() ;
;
(Ⅲ)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙、丁、戌5人参加社区志愿者服务活动,每人从事团购、体温测量、进出人员信息登记、司机四项工作之一,每项工作至少有一人参加.若甲、乙不会开车但能从事其他三项工作,丙、丁、戌都能胜任四项工作,则不同安排方案的种数是( )
A.234B.152C.126D.108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的体积为1.在侧棱
的体积为1.在侧棱![]() 上取一点
上取一点![]() ,使
,使![]() ,然后在
,然后在![]() 上取一点
上取一点![]() ,使
,使![]() ,继续在
,继续在![]() 上取一点
上取一点![]() ,使
,使![]() ,……按上述步骤,依次得到点
,……按上述步骤,依次得到点![]() ,记三棱锥
,记三棱锥![]() 的体积依次构成数列
的体积依次构成数列![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() .
.

(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,若不等式
项和,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() .
.
(1)若a=4,求函数f(x)的单调区间;
(2)若函数f(x)在区间(0,1]内单调递增,求实数a的取值范围;
(3)若x1、x2∈R+,且x1≤x2,求证:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com