练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    观察下列各式：a＋b＝1，a2＋b2＝3，a3＋b3＝4，a4＋b4＝7，a5＋b5＝11，…，则a10＋b10＝(　　)

    A．28                          B．76

    C．123                         D．199


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设数列{an}的前n项和为Sn，满足2Sn＝an＋1－2n＋1＋1，n∈N*，且a1，a2＋5，a3成等差数列．

    (1)求a1的值；

    (2)求数列{an}的通项公式；

    (3)证明：对一切正整数n，有＜.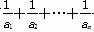

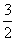    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在R上定义运算⊙：a⊙b＝ab＋2a＋b，则满足x⊙(x－2)＜0的实数x的取值范围为(　　)

    A．(0,2)                          B．(－2,1)

    C．(－∞，－2)∪(1，＋∞)         D．(－1,2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设z＝x＋y，其中x，y满足，当z的最大值为6时，k的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一切奇数都不能被2整数，2100＋1是奇数，所以2100＋1不能被2整除，其演绎“三段论”的形式为：

    大前提：一切奇数都不能被2整除，

    小前提：________________________________________________________________________，

    结论：________________________________________________________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝lg2＋lg5，b＝ex(x<0)，则a与b大小关系为(　　)

    A．a>b　　　　　　　　　　        B．a<b

    C．a＝b                           D．a≤b

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    α，β，γ是三个平面，a，b是两条直线，有下列三个条件：

    ①a∥γ，b⊂β；②a∥γ，b∥β；③b∥β，a⊂γ.

    如果命题“α∩β＝a，b⊂γ，且________，则a∥b”为真命题．(填序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    是否存在常数a，b，c使得等式1·22＋2·32＋…＋n(n＋1)2＝ (an2＋bn＋c)对于一切正整数n都成立？并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面α、β相交，在α、β内各取两点，这四点都不在交线上，这四点能确定________个平面．

    查看答案和解析>>

    同步练习册答案