
设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有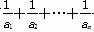 <
<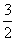 .
.
解:(1 )∵a1,a2+5,a3成等差数列,
)∵a1,a2+5,a3成等差数列,
∴2(a2+5)=a1+a3.
又∵2a1 =2S1=a2-22+1,2(a1+a2)
=2S1=a2-22+1,2(a1+a2) =2S2=a3-23+1,
=2S2=a3-23+1,
∴a2=2a1+3,a3=6a1+13.
因此4a1+16=7a1+13,从而a1=1.
(2)由题设条件知,n≥2时,2Sn-1=an-2n+1,
2Sn=an+1-2n+1+1.
∴2an=an+1-an-2n,于是
an+1=3an+2n(n≥2).
而由(1)知,a2=2a1+3=5=3a1+2,
因此对一切正整数n,有an+1=3an+2n,
所以an+1+2n +1=3(an+2n).
+1=3(an+2n).
又∵a1+21=3,
∴{an+2n}是以3为首项,3为公比的等比数列.
故an+2n=3n,即an=3n-2n.
(3)证明:∵an=3n-2n=3·3n-1-2n=3n-1+2(3n-1-2n-1)≥3n-1,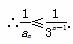
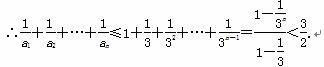


科目:高中数学 来源: 题型:
等差数列{an}的前n项和为Sn,S9=-18, S13=-52,等比数列{bn}中,b5=a5,b7=a7,则b15的值为( )
S13=-52,等比数列{bn}中,b5=a5,b7=a7,则b15的值为( )
A.64 B.-64
C.128 D.-128
查看答案和解析>>
科目:高中数学 来源: 题型:
某商场因管理不善及场内设施陈旧,致使年底结算亏损,决定从今年开始投入资金进行整修,计划第一个月投入80万元,以后每月投入将比上月减少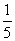 .第一个月的经营收入约为40万元,预计以后每个月收入会比上个月增加
.第一个月的经营收入约为40万元,预计以后每个月收入会比上个月增加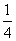 .
.
(1)设n个月内的总投入为an万元,总收入为bn万元,写出an,bn;
(2)问经过几个月后商场开始扭亏为盈.
查看答案和解析>>
科目:高中数学 来源: 题型:
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
A.28 B. 76
76
C.123 D.199
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com