
分析 (1)根据所给的二次函数的性质,求出对称轴,讨论对称轴和区间的关系,运用单调性即可求得最值,进而得到函数g(b)的解析式;
(2)根据(1)求得的结果,-x2-bx+3=|b2+b-2|,0<b<1,利用二次函数在定区间上的最值的求法,以及绝对值函数的单调性求得值域,再由任意和存在性问题的解法,即可求出b的范围..
解答 解:(1)f(x)=(x+$\frac{b}{2}$)2-3-$\frac{{b}^{2}}{4}$,
抛物线开口向上,其对称轴方程为x=-$\frac{b}{2}$,
由b2<b,可得0<b<1,-$\frac{b}{2}$<0,
即有f(x)在[b2,b]上递增,可得
m(b)=b4+b3-3,M(b)=2b2-3,
即有g(b)=M(b)-m(b)=2b2-b4-b3,(0<b<1);
(2)对任意的x∈[b2,b],
都存在符合题意b,使得-b2f(x)=|g(b)|成立,
可得-x2-bx+3=|b2+b-2|,0<b<1,
由0<b<1可得-x2-bx+3在[b2,b]递减,
即有值域为[3-2b2,3-b4-b3],
又|b2+b-2|在0<b<1的值域为(0,2),
由题意可得0<3-2b2<3-b4-b3<2,
由b4+b3>1,令h(b)=b4-b3,由h(0.8)<1,h(0.9)>1,
可得h(b)=1的根为t(0.8<t<0.9),
综上可得b的范围是(t,1),(0.8<t<0.9).
点评 本题考查二次函数的性质,注意讨论对称轴与区间的关系,同时考查函数的单调性的运用,以及任意和存在性问题的解法,注意转化为求函数的值域问题,是一个易错题,属中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
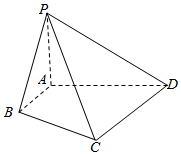 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{7}{6}]$ | B. | $[\frac{14}{9},+∞)$ | C. | $[\frac{14}{9},7]$ | D. | $[\frac{7}{6},\frac{14}{9}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com