
【题目】已知向量a=(cosx,sinx),b=(-cosx,cosx),c=(-1,0).
(1)若x=![]() ,求向量a,c的夹角;
,求向量a,c的夹角;
(2)当x∈![]() 时,求函数f(x)=2a·b+1的值域.
时,求函数f(x)=2a·b+1的值域.
【答案】(1)![]() (2)[-
(2)[-![]() ,1]
,1]
【解析】(1)试题分析:根据公式cos〈a,c〉=![]() 代入数值计算(2)先化简f(x)=2a·b+1=
代入数值计算(2)先化简f(x)=2a·b+1=![]() sin
sin![]() ,然后求出2x-
,然后求出2x-![]() ∈
∈![]() ,再根据函数图形便可得到当2x-
,再根据函数图形便可得到当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)max=1 当2x-
时,f(x)max=1 当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)min=-
时,f(x)min=-![]()
试题解析:
解:(1)∵a=(cosx,sinx),c=(-1,0),
∴|a|=![]() =1,|c|=
=1,|c|=![]() =1.
=1.
当x=![]() 时,a=
时,a=![]() =
=![]() ,
,
a·c=![]() ×(-1)+
×(-1)+![]() ×0=-
×0=-![]() ,cos〈a,c〉=
,cos〈a,c〉=![]() =-
=-![]() .
.
∵0≤〈a,c〉≤π,∴〈a,c〉=![]()
(2)f(x)=2a·b+1=2(-cos2x+sinxcosx)+1
=2sinxcosx-(2cos2x-1)=sin2x-cos2x
=![]() sin
sin![]()
∵x∈![]() ,∴2x-
,∴2x-![]() ∈
∈![]() ,
,
故sin![]() ∈
∈![]() ,
,
∴当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)max=1
时,f(x)max=1
当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)min=-
时,f(x)min=-![]()
∴f(x)的值域为[-![]() ,1]
,1]


科目:高中数学 来源: 题型:
【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入![]() 万元,以后每年投入将比上年减少
万元,以后每年投入将比上年减少![]() .本年度当地旅游业收入估计为
.本年度当地旅游业收入估计为![]() 万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加![]() .
.
(Ⅰ)设![]() 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为![]() 万元,旅游业总收入为
万元,旅游业总收入为![]() 万元.写出
万元.写出![]() 的表达式;
的表达式;
(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是_______(填序号)
①命题“![]() 有
有![]() ”的否定是“
”的否定是“![]() 有
有![]() ”;
”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知![]() ,
, ![]() ,若命题
,若命题![]() 为真命题,则
为真命题,则![]() 的取值范围是
的取值范围是![]() ;
;
④“![]() ”是“
”是“![]() ”成立的充分条件.
”成立的充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,椭圆C与y轴交于A、B两点,|AB|=2.
,椭圆C与y轴交于A、B两点,|AB|=2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点P是椭圆C上的动点,且直线PA,PB与直线x=4分别交于M、N两点,是否存在点P,使得以MN为直径的圆经过点(2,0)?若存在,求出点P的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c已知b=4,c=5,A=60°.
(1)求边长a和△ABC的面积;
(2)求sin2B的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
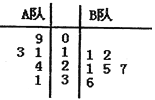
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com