
| A. | 2 | B. | $\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
分析 利用两个向量数量积的定义与模长公式,进行计算即可.
解答 解:平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×1×cos120°=-1.
∴${(\overrightarrow{a}+2\overrightarrow{b})}^{2}$=${\overrightarrow{a}}^{2}$+4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$
=22+4×(-1)+4×12
=4,
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2.
故选:A.
点评 本题主要考查两个向量数量积的定义与求向量的模应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
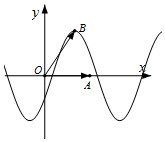 直角坐标系xOy中,已知点A(1,0),函数f(x)=sin(2x-$\frac{π}{6}$)的图象在y轴右侧的第一个最高点为B,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$.
直角坐标系xOy中,已知点A(1,0),函数f(x)=sin(2x-$\frac{π}{6}$)的图象在y轴右侧的第一个最高点为B,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{{{n^2}+n}}{2}$ | B. | an=$\frac{{{n^2}-n}}{2}$ | C. | an=n2-n+1 | D. | an=n2+n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
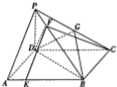 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com