
科目:高中数学 来源: 题型:
已知曲线 的极坐标方程是
的极坐标方程是 ,直线的参数方程是
,直线的参数方程是 (为参数).
(为参数).
(Ⅰ)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线与 轴的交点是
轴的交点是 ,
,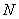 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1,记函数f(x)的定义域为D.
(1)求函数f(x)的定义域D;
(2)若函数f(x)的最小值为﹣4,求a的值;
(3)若对于D内的任意实数x,不等式﹣x2+2mx﹣m2+2m<1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的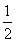 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用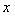 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数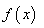 .⑴试规定
.⑴试规定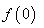 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数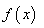 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设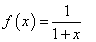 ,现有
,现有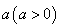 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于定义域为D的函数f(x),若存在区间M=[a,b]⊆D(a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的“等值区间”.给出下列三个函数:①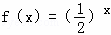 ; ②f(x)=x3; ③f(x)=log2x+1
; ②f(x)=x3; ③f(x)=log2x+1
则存在“等值区间”的函数的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合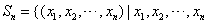 是正整数
是正整数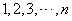 的一个排列
的一个排列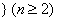 ,函数
,函数
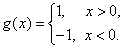
对于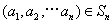 ,定义:
,定义: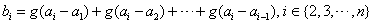 ,
,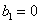 ,称
,称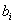 为
为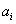 的满意指数.排列
的满意指数.排列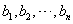 为排列
为排列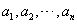 的生成列.
的生成列.
(Ⅰ)当 时,写出排列
时,写出排列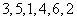 的生成列;
的生成列;
(Ⅱ)证明:若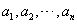 和
和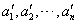 为
为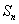 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于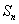 中的排列
中的排列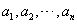 ,进行如下操作:将排列
,进行如下操作:将排列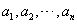 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加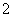 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com