
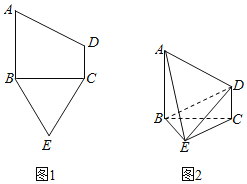
【题目】已知五边形ABECD有一个直角梯形ABCD与一个等边三角形BCE构成,如图1所示,![]() ,且
,且![]() ,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且
,将梯形ABCD沿着BC折起,形成如图2所示的几何体,且![]() 平面BEC.
平面BEC.
![]() 求证:平面
求证:平面![]() 平面ADE;
平面ADE;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() .
.
(1)当![]() 时,试确定曲线
时,试确定曲线![]() 的形状及其焦点坐标;
的形状及其焦点坐标;
(2)若直线![]() 交曲线
交曲线![]() 于点
于点![]() 、
、![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,试问此时曲线
,试问此时曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?
对称?
(3)当![]() 为大于1的常数时,设
为大于1的常数时,设![]() 是曲线
是曲线![]() 上的一点,过点
上的一点,过点![]() 作一条斜率为
作一条斜率为![]() 的直线
的直线![]() ,又设
,又设![]() 为原点到直线
为原点到直线![]() 的距离,
的距离,![]() 分别为点
分别为点![]() 与曲线
与曲线![]() 两焦点的距离,求证
两焦点的距离,求证![]() 是一个定值,并求出该定值.
是一个定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解共享单车的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率分布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值;
(2)求这50名问卷评分数据的中位数;
(3)估计样本的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆![]() 与双曲线
与双曲线![]() (
(![]() ,
,![]() )有公共焦点,现一光线从它们的左焦点出发,在椭圆与双曲线间连续反射,则光线经过
)有公共焦点,现一光线从它们的左焦点出发,在椭圆与双曲线间连续反射,则光线经过![]() 次反射后,首次回到左焦点所经过的路径长为______.
次反射后,首次回到左焦点所经过的路径长为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() 时按
时按![]() 计算)需再收
计算)需再收![]() 元.公司从承揽过的包裹中,随机抽取
元.公司从承揽过的包裹中,随机抽取![]() 件,其重量统计如下:
件,其重量统计如下:

公司又随机抽取了![]() 天的揽件数,得到频数分布表如下:
天的揽件数,得到频数分布表如下:

以记录的![]() 天的揽件数的频率作为各揽件数发生的概率
天的揽件数的频率作为各揽件数发生的概率
![]() 计算该公司
计算该公司![]() 天中恰有
天中恰有![]() 天揽件数在
天揽件数在![]() 的概率;
的概率;
![]() 估计该公司对每件包裹收取的快递费的平均值;
估计该公司对每件包裹收取的快递费的平均值;
![]() 公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员
公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,每人每天工资
件,每人每天工资![]() 元,公司正在考虑是否将前台工作人员裁减
元,公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?(同一组中的揽件数以这组数据所在区间中点值作代表)
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?(同一组中的揽件数以这组数据所在区间中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线外一点M作抛物线的两条切线,两切点的连线段称为点M对应的切点弦已知抛物线为![]() ,点P,Q在直线l:
,点P,Q在直线l:![]() 上,过P,Q两点对应的切点弦分别为AB,CD
上,过P,Q两点对应的切点弦分别为AB,CD
![]() 当点P在l上移动时,直线AB是否经过某一定点,若有,请求出该定点的坐标;如果没有,请说明理由
当点P在l上移动时,直线AB是否经过某一定点,若有,请求出该定点的坐标;如果没有,请说明理由
![]() 当
当![]() 时,点P,Q在什么位置时,
时,点P,Q在什么位置时,![]() 取得最小值?
取得最小值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com