
【题目】设数列{an}是各项均为正数的等比数列,其前n项和为Sn , 若a1a5=64,S5﹣S3=48.
(1)求数列{an}的通项公式;
(2)对于正整数k,m,l(k<m<l),求证:“m=k+1且l=k+3”是“5ak , am , al这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列{bn}满足:对任意的正整数n,都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6,且集合 ![]() 中有且仅有3个元素,试求λ的取值范围.
中有且仅有3个元素,试求λ的取值范围.
【答案】
(1)解:设等比数列{an}的公比是q,
∵数列{an}是各项均为正数的等比数列,∴ ![]() ,解得a3=8,
,解得a3=8,
又∵S5﹣S3=48,∴ ![]() ,解得q=2,
,解得q=2,
∴ ![]() ;
;
(2)解:(ⅰ)必要性:设5ak,am,al这三项经适当排序后能构成等差数列,
①若25ak=am+al,则102k=2m+2l,∴10=2m﹣k+2l﹣k,∴5=2m﹣k﹣1+2l﹣k﹣1,
∴ ![]() ,∴
,∴ ![]() .
.
②若2am=5ak+al,则22m=52k+2l,∴2m+1﹣k﹣2l﹣k=5,左边为偶数,等式不成立,
③若2al=5ak+am,同理也不成立,
综合①②③,得m=k+1,l=k+3,所以必要性成立
(ⅱ)充分性:设m=k+1,l=k+3,
则5ak,am,al这三项为5ak,ak+1,ak+3,即5ak,2ak,8ak,
调整顺序后易知2ak,5ak,8ak成等差数列,
所以充分性也成立.
综合(ⅰ)(ⅱ),原命题成立
(3)解:因为 ![]() ,
,
即 ![]() ,①
,①
∴当n≥2时, ![]() ,②
,②
则②式两边同乘以2,得 ![]() ,③
,③
∴①﹣③,得2bn=4n﹣2,即bn=2n﹣1(n≥2),
又当n=1时, ![]() ,即b1=1,适合bn=2n﹣1(n≥2),
,即b1=1,适合bn=2n﹣1(n≥2),
∴bn=2n﹣1.…14分
∴ ![]() ,∴
,∴ ![]() ,
,
∴n=2时, ![]() ,即
,即 ![]() ;
;
∴n≥3时, ![]() ,此时
,此时 ![]() 单调递减,
单调递减,
又 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,∴
,∴ ![]() .
.
【解析】1、根据等比数列中项的性质得到a 1 a 5 = a 3 2 = 64,得到a3=8,再根据S5﹣S3=a 4+ a 5 =48解得q=2得到等比数列的通项公式。
2、由已知可得先证明必要性,利用an都是整数的性质分别讨论5ak,,am, al不同的排序情况。充分性,适当对5ak,,am, al进行排列可得结论。
3、根据对递推公式的变换求出数列{bn}的通项公式再通过数列{![]() }
}![]() 的通项公式判断该数列的单调性进而确定M的元素即得出
的通项公式判断该数列的单调性进而确定M的元素即得出![]() 的取值范围。
的取值范围。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若满足
,若满足 ![]() ,则称数列
,则称数列 ![]() 为“
为“ ![]() 数列”.
数列”.
若存在一个正整数 ![]() ,若数列
,若数列 ![]() 中存在连续的
中存在连续的 ![]() 项和该数列中另一个连续的
项和该数列中另一个连续的 ![]() 项恰好按次序对应相等,则称数列
项恰好按次序对应相等,则称数列 ![]() 是“
是“ ![]() 阶可重复数列”,
阶可重复数列”,
例如数列 ![]() 因为
因为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,所以数列
按次序对应相等,所以数列 ![]() 是“
是“ ![]() 阶可重复数列”.
阶可重复数列”.
(I)分别判断下列数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .是否是“
.是否是“ ![]() 阶可重复数列”?如果是,请写出重复的这
阶可重复数列”?如果是,请写出重复的这 ![]() 项;
项;
(II)若项数为 ![]() 的数列
的数列 ![]() 一定是 “
一定是 “ ![]() 阶可重复数列”,则
阶可重复数列”,则 ![]() 的最小值是多少?说明理由;
的最小值是多少?说明理由;
(III)假设数列 ![]() 不是“
不是“ ![]() 阶可重复数列”,若在其最后一项
阶可重复数列”,若在其最后一项 ![]() 后再添加一项
后再添加一项 ![]() 或
或 ![]() ,均可 使新数列是“
,均可 使新数列是“ ![]() 阶可重复数列”,且
阶可重复数列”,且 ![]() ,求数列
,求数列 ![]() 的最后一项
的最后一项 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列结论中: ①函数y=sin(kπ﹣x)(k∈Z)为奇函数;
②函数 ![]() 的图象关于点
的图象关于点 ![]() 对称;
对称;
③函数 ![]() 的图象的一条对称轴为
的图象的一条对称轴为 ![]() π;
π;
④若tan(π﹣x)=2,则cos2x= ![]() .
.
其中正确结论的序号为(把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知a(sinA﹣sinB)=(c﹣b)(sinC+sinB) (Ⅰ)求角C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.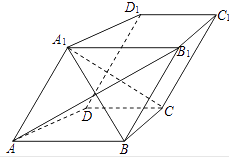
(1)求证:AB∥平面D1DCC1;
(2)求证:AB1⊥平面A1BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线Ω:x2=2py(p>0),过点(0,2p)的直线与抛物线Ω交于A、B两点,AB的中点为M,若点M到直线y=2x的最小距离为 ![]() ,则p=( )
,则p=( )
A.![]()
B.1
C.![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com