
【题目】对于数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若满足
,若满足 ![]() ,则称数列
,则称数列 ![]() 为“
为“ ![]() 数列”.
数列”.
若存在一个正整数 ![]() ,若数列
,若数列 ![]() 中存在连续的
中存在连续的 ![]() 项和该数列中另一个连续的
项和该数列中另一个连续的 ![]() 项恰好按次序对应相等,则称数列
项恰好按次序对应相等,则称数列 ![]() 是“
是“ ![]() 阶可重复数列”,
阶可重复数列”,
例如数列 ![]() 因为
因为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,所以数列
按次序对应相等,所以数列 ![]() 是“
是“ ![]() 阶可重复数列”.
阶可重复数列”.
(I)分别判断下列数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .是否是“
.是否是“ ![]() 阶可重复数列”?如果是,请写出重复的这
阶可重复数列”?如果是,请写出重复的这 ![]() 项;
项;
(II)若项数为 ![]() 的数列
的数列 ![]() 一定是 “
一定是 “ ![]() 阶可重复数列”,则
阶可重复数列”,则 ![]() 的最小值是多少?说明理由;
的最小值是多少?说明理由;
(III)假设数列 ![]() 不是“
不是“ ![]() 阶可重复数列”,若在其最后一项
阶可重复数列”,若在其最后一项 ![]() 后再添加一项
后再添加一项 ![]() 或
或 ![]() ,均可 使新数列是“
,均可 使新数列是“ ![]() 阶可重复数列”,且
阶可重复数列”,且 ![]() ,求数列
,求数列 ![]() 的最后一项
的最后一项 ![]() 的值.
的值.
【答案】解:(I) ![]()
(Ⅱ)因为数列 ![]() 的每一项只可以是
的每一项只可以是 ![]() 或
或 ![]() ,所以连续
,所以连续 ![]() 项共有
项共有 ![]() 种不同的情形.
种不同的情形.
若 ![]() ,则数列
,则数列 ![]() 中有
中有 ![]() 组连续
组连续 ![]() 项,则这其中至少有两组按次序对应相等,即项数为
项,则这其中至少有两组按次序对应相等,即项数为 ![]() 的数列
的数列 ![]() 一定是“
一定是“ ![]() 阶可重复数列”;
阶可重复数列”;
若 ![]() ,数列
,数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 不是“
不是“ ![]() 阶可重复数列”;则
阶可重复数列”;则 ![]() 时,均存在不是“
时,均存在不是“ ![]() 阶可重复数列”的数列
阶可重复数列”的数列 ![]() .
.
所以要使数列 ![]() 一定是“
一定是“ ![]() 阶可重复数列”,则
阶可重复数列”,则 ![]() 的最小值是
的最小值是 ![]() .
.
(III)由于数列 ![]() 在其最后一项
在其最后一项 ![]() 后再添加一项
后再添加一项 ![]() 或
或 ![]() ,均可使新数列是“
,均可使新数列是“ ![]() 阶可重复数列”,即在数列
阶可重复数列”,即在数列 ![]() 的末项
的末项 ![]() 后再添加一项
后再添加一项 ![]() 或
或 ![]() ,
,
则存在 ![]() ,使得
,使得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,或
按次序对应相等,或 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,如果
按次序对应相等,如果 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 不能按次序对应相等,
不能按次序对应相等,
那么必有 ![]() ,
, ![]() ,
, ![]() ,使得
,使得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等.
按次序对应相等.
此时考虑 ![]() ,
, ![]() 和
和 ![]() ,其中必有两个相同,这就导致数列
,其中必有两个相同,这就导致数列 ![]() 中有两个连续的五项恰按次序对应相等,从而数列
中有两个连续的五项恰按次序对应相等,从而数列 ![]() 是“
是“ ![]() 阶可重复数列”,这和题设中数列
阶可重复数列”,这和题设中数列 ![]() 不是“
不是“ ![]() 阶可重复数列”矛盾!
阶可重复数列”矛盾!
所以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,从而
按次序对应相等,从而 ![]()
【解析】(1)由题意观察可得该数列是5阶可重复数列。(2)根据题意列验证举即可得出数列 { an } 一定是“ 3 阶可重复数列”,则 m 的最小值是 11。(3)根据题意利用假设法结合已知推导出数列 { an } 是“ 5 阶可重复数列”,这和题设中数列 { an } 不是“ 5 阶可重复数列”矛盾进而得出假设不成立即得结果。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2的图象经过点M(1,4),且在x=﹣2取得极值.
( I)求实数a,b的值;
( II)若函数f(x)在区间(m,m+1)上不单调,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过椭圆C: ![]() 的左顶点A作直线l,与椭圆C和y轴正半轴分别交于点P,Q.
的左顶点A作直线l,与椭圆C和y轴正半轴分别交于点P,Q.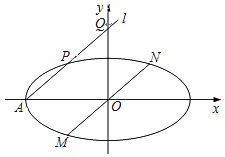
(1)若AP=PQ,求直线l的斜率;
(2)过原点O作直线l的平行线,与椭圆C交于点M,N,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了 ![]() 次涨停(每次上涨
次涨停(每次上涨 ![]() ),又经历了
),又经历了 ![]() 次跌停(每次下跌
次跌停(每次下跌 ![]() ),则该股民这只股票的盈亏情况(不考虑其他费用)是( )
),则该股民这只股票的盈亏情况(不考虑其他费用)是( )
A.略有盈利
B.略有亏损
C.没有盈利也没有亏损
D.无法判断盈亏情况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在(1+x+x2)n= ![]() x
x ![]() x2+…
x2+… ![]() xr+…
xr+… ![]() x2n﹣1
x2n﹣1 ![]() x2n的展开式中,把D
x2n的展开式中,把D ![]() ,D
,D ![]() ,D
,D ![]() …,D
…,D ![]() …,D
…,D ![]() 叫做三项式系数
叫做三项式系数
(1)求D ![]() 的值
的值
(2)根据二项式定理,将等式(1+x)2n=(1+x)n(x+1)n的两边分别展开可得,左右两边xn的系数相等,即C ![]() =(C
=(C ![]() )2+(C
)2+(C ![]() )2+(C
)2+(C ![]() )2+…+(C
)2+…+(C ![]() )2 , 利用上述思想方法,请计算D
)2 , 利用上述思想方法,请计算D ![]() C
C ![]() ﹣D
﹣D ![]() C
C ![]() +D
+D ![]() C
C ![]() ﹣…+(﹣1)rD
﹣…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x, ![]() .
.
(1)求h(x)的最大值;
(2)若关于x的不等式xf(x)≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,求实数a的取值范围;
(3)若关于x的方程f(x)﹣x3+2ex2﹣bx=0恰有一解,其中e是自然对数的底数,求实数b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中:
①双曲线 ![]() 与椭圆
与椭圆 ![]() 有相同的焦点;
有相同的焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设A,B为两个定点,k为常数,若|PA|﹣|PB|=k,则动点P的轨迹为双曲线;
④过定圆C上一点A作圆的动弦AB,O为原点,若 ![]() 则动点P的轨迹为椭圆.其中正确的个数是( )
则动点P的轨迹为椭圆.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是各项均为正数的等比数列,其前n项和为Sn , 若a1a5=64,S5﹣S3=48.
(1)求数列{an}的通项公式;
(2)对于正整数k,m,l(k<m<l),求证:“m=k+1且l=k+3”是“5ak , am , al这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列{bn}满足:对任意的正整数n,都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6,且集合 ![]() 中有且仅有3个元素,试求λ的取值范围.
中有且仅有3个元素,试求λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com