
【题目】如图,在平面直角坐标系xOy中,过椭圆C: ![]() 的左顶点A作直线l,与椭圆C和y轴正半轴分别交于点P,Q.
的左顶点A作直线l,与椭圆C和y轴正半轴分别交于点P,Q.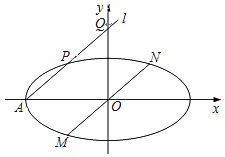
(1)若AP=PQ,求直线l的斜率;
(2)过原点O作直线l的平行线,与椭圆C交于点M,N,求证: ![]() 为定值.
为定值.
【答案】
(1)解:A(﹣2,0),设Q(0,m)(m>0),
∵AP=PQ,∴P(﹣1, ![]() ),
),
代入椭圆方程得: ![]() =1,
=1,
解得m= ![]() ,
,
∴直线l的斜率为 ![]()
(2)证明:设直线l的斜率为k(k> ![]() ),直线l的方程为:y=k(x+2),
),直线l的方程为:y=k(x+2),
令x=0得y=2k,即Q(0,2k),
∴AQ= ![]() =2
=2 ![]() .
.
联立方程组 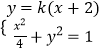 ,消元得:(1+4k2)x2+16k2x+16k2﹣4=0,
,消元得:(1+4k2)x2+16k2x+16k2﹣4=0,
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∴AP= ![]()
![]() =
= ![]() .
.
∴APAQ= ![]() .
.
直线MN的方程为y=kx,
联立方程组 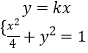 ,得(1+4k2)x2﹣4=0,
,得(1+4k2)x2﹣4=0,
设N(x3,y3),M(﹣x3,﹣y3),
则 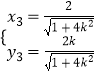 ,
,
∴MN=2ON=2 ![]() =4
=4 ![]() ,
,
∴ ![]() =
= ![]()
![]() =
= ![]() .
.
∴ ![]() 为定值
为定值
【解析】(1)根据题意设出点Q的坐标,然后利用中点坐标公式将点P的坐标用点A、点Q的坐标表示,并代入椭圆方程求出点Q的坐标后即可求解;


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|y= ![]() },集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
},集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
(1)求A∩B;
(2)若A∪C=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e|x| , 将函数f(x)的图象向右平移3个单位后,再向上平移2个单位,得到函数g(x)的图象,函数h(x)= ![]() 若对于任意的x∈[3,λ](λ>3),都有h(x)≥g(x),则实数λ的最大值为 .
若对于任意的x∈[3,λ](λ>3),都有h(x)≥g(x),则实数λ的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)与g(x)的图象关于原点对称,且它们的图象拼成如图所示的“Z”形折线段ABOCD,不含A(0,1),B(1,1),O(0,0),C(﹣1,﹣1),D(0,﹣1)五个点.则满足题意的函数f(x)的一个解析式为 . 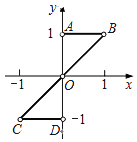
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明设置的手机开机密码若连续3次输入错误,则手机被锁定,5分钟后,方可重新输入.某日,小明忘记了开机密码,但可以确定正确的密码是他常用的4个密码之一,于是,他决定逐个(不重复)进行尝试.
(1)求手机被锁定的概率;
(2)设第X次输入后能成功开机,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景点拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为36米,其中大圆弧所在圆的半径为14米,设小圆弧所在圆的半径为x米,圆心角为θ(弧度).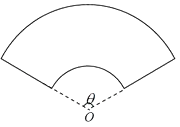
(1)求θ关于x的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为16元/米,设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,若满足
,若满足 ![]() ,则称数列
,则称数列 ![]() 为“
为“ ![]() 数列”.
数列”.
若存在一个正整数 ![]() ,若数列
,若数列 ![]() 中存在连续的
中存在连续的 ![]() 项和该数列中另一个连续的
项和该数列中另一个连续的 ![]() 项恰好按次序对应相等,则称数列
项恰好按次序对应相等,则称数列 ![]() 是“
是“ ![]() 阶可重复数列”,
阶可重复数列”,
例如数列 ![]() 因为
因为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 按次序对应相等,所以数列
按次序对应相等,所以数列 ![]() 是“
是“ ![]() 阶可重复数列”.
阶可重复数列”.
(I)分别判断下列数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .是否是“
.是否是“ ![]() 阶可重复数列”?如果是,请写出重复的这
阶可重复数列”?如果是,请写出重复的这 ![]() 项;
项;
(II)若项数为 ![]() 的数列
的数列 ![]() 一定是 “
一定是 “ ![]() 阶可重复数列”,则
阶可重复数列”,则 ![]() 的最小值是多少?说明理由;
的最小值是多少?说明理由;
(III)假设数列 ![]() 不是“
不是“ ![]() 阶可重复数列”,若在其最后一项
阶可重复数列”,若在其最后一项 ![]() 后再添加一项
后再添加一项 ![]() 或
或 ![]() ,均可 使新数列是“
,均可 使新数列是“ ![]() 阶可重复数列”,且
阶可重复数列”,且 ![]() ,求数列
,求数列 ![]() 的最后一项
的最后一项 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com